题目内容

10．化简：$\frac{2}{2-\sqrt{2}}$=2+$\sqrt{2}$．

分析 根据有理化因式的定义：两个根式相乘的积不含根号，即可判断．

解答 解：原式=$\frac{2（2+\sqrt{2}）}{（2-\sqrt{2}）（2+\sqrt{2}）}$=2+$\sqrt{2}$，
故答案为：2+$\sqrt{2}$．

点评 本题考查了分母有理化，正确选择两个二次根式，使它们的积符合平方差公式是解答问题的关键．

练习册系列答案
相关题目
17．在实数-2，$\sqrt{2}$，0，-1中，最小的数是（　　）
A．-2B．$\sqrt{2}$C．0D．-1
1．已知$\sqrt{5.691}$≈2.386，而$\sqrt{x}≈$0.02386，则x=0.0006（保留到万分位）．
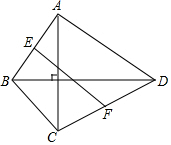18．在四边形ABCD中，对角线AC⊥BD且AC=4、BD=6．E、F分别是边AB、CD的中点，则EF=$\sqrt{13}$．
5．已知-1＜x＜0，化简：$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}-2}+\sqrt{{x}^{2}+\frac{1}{{x}^{2}}+2}$．
15．计算：-14+|-$\frac{1}{2}$|-（-$\frac{3}{2}$）0×（-$\frac{2}{3}$）
2．已知x=$\sqrt{2}$+1，y=$\sqrt{2}$-1，则x2-5xy+y2+6等于（　　）
A．5B．7C．9D．11
19．计算：$2\sqrt{2}×3\sqrt{5}÷5\sqrt{2\frac{1}{3}}$．
20．在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，CD=4，AC=6，则CB=2$\sqrt{7}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网