题目内容
20.在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,AC=6,则CB=2$\sqrt{7}$.分析 由直角三角形斜边上的中线性质得出AB=8,由勾股定理求出CB即可.
解答 解:∵Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,
∴AB=2CD=8,
∴CB=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{8}^{2}-{6}^{2}}$=2$\sqrt{7}$;
故答案为:2$\sqrt{7}$.
点评 本题考查了勾股定理和直角三角形斜边上中线的性质,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
12.若函数y=mx2+(m-1)x+$\frac{1}{2}$(m-1)的图象与x轴只有一个交点,那么m的值是( )
| A. | 0 | B. | 0,-1或1 | C. | 1或-1 | D. | 0或1 |
10.在一年一度的国家学生体质测试中,金星中学对全校2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并绘制成统计表,绘制成频数直方图.
(1)在这个问题中,总体是什么?
(2)直接写出a,b,c,d的值.
(3)补全频数直方图.
(4)初中毕业生体能测试项目成绩评定标准是男生1000m不超过4′20″(即260秒)为合格,你能估计出该校初中男生的1000m的合格人数吗?如果能,请求出合格的人数;如果不能,请说明理由.

| 序号 | 范围(单位:秒) | 频数 | 频率 |
| 1 | 170<x≤200 | 5 | 0.1 |
| 2 | 200<x≤230 | 13 | a |
| 3 | 230<x≤260 | 15 | 0.3 |
| 4 | 260<x≤290 | c | d |
| 5 | 290<x≤320 | 5 | 0.1 |
| 6 | 320<x≤350 | 2 | 0.04 |
| 7 | 350<x≤380 | 2 | 0.04 |
| 合计 | b | 1.00 |
(2)直接写出a,b,c,d的值.
(3)补全频数直方图.
(4)初中毕业生体能测试项目成绩评定标准是男生1000m不超过4′20″(即260秒)为合格,你能估计出该校初中男生的1000m的合格人数吗?如果能,请求出合格的人数;如果不能,请说明理由.
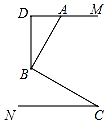 如图,已知AM∥CN,点B为平面内一点,AB⊥BC于B.过点B作BD⊥AM于点D,则图中∠ABD和∠C的关系是∠ABD=∠C.
如图,已知AM∥CN,点B为平面内一点,AB⊥BC于B.过点B作BD⊥AM于点D,则图中∠ABD和∠C的关系是∠ABD=∠C.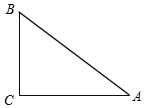 在Rt△ABC中,∠C=90°,AC=4,BC=3,
在Rt△ABC中,∠C=90°,AC=4,BC=3,