题目内容
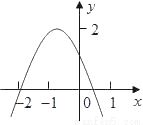
在平面直角坐标系xoy中,抛物线y=ax2+bx+c (a≠O)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(-4,O),抛物线的对称轴是直线x=-3,且经过A、C两点的直线为y=kx+4.
(1)求抛物线的函数表达式;
(2)将直线AC向下平移m个单位长度后,得到的直线l与抛物线只有一个交点D,求m的值;
(3)抛物线上是否存在点Q,使点Q到直线AC的距离为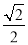 ?若存在,请直接写出Q的坐标,若不存在,请说明理由.
?若存在,请直接写出Q的坐标,若不存在,请说明理由.
练习册系列答案
相关题目


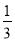 ,b=3.
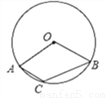
,b=3.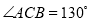 ,则圆心角
,则圆心角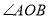 =( )
=( )
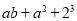 的次数是__________.
的次数是__________.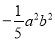 ,
, 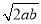 ,
, 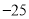 ,
, 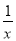 ,
, 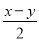 ,
, 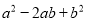 中单项式的个数有( )
中单项式的个数有( )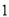 个 B.
个 B. 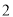 个 C.
个 C. 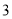 个 D.
个 D. 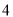 个
个