题目内容
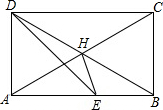 如图,在矩形ABCD中,对角线DB=2AD,DE平分∠CDA,求∠HED的度数.
如图,在矩形ABCD中,对角线DB=2AD,DE平分∠CDA,求∠HED的度数.考点:矩形的性质
专题:
分析:先根据矩形性质证明HA=HC=HB=HD,证出AD=AE,再证明△ADH是等边三角形,证出AE=AH,∠HAE=30°,求出∠AEH=75°,即可求出∠HED.
解答:
解:∵四边形ABCD是矩形,
∴HA=HC=
AC,HD=HB=
BD,AC=BD,∠ADC=∠DAB=90°,
∴HA=HC=HB=HD,
∵DE平分∠CDA,
∴∠ADE=45°,
∴∠AED=90°-45°=45°,
∴AD=AE,
∵DB=2AD,
∴HA=AD=HD,
∴∠DAH=60°,AE=AH,
∴∠HAE=90°-60°=30°,
∴∠AEH=
(180°-30°)=75°,
∴∠HED=75°-45°=30°.
∴HA=HC=
| 1 |
| 2 |
| 1 |
| 2 |
∴HA=HC=HB=HD,
∵DE平分∠CDA,
∴∠ADE=45°,
∴∠AED=90°-45°=45°,
∴AD=AE,
∵DB=2AD,
∴HA=AD=HD,
∴∠DAH=60°,AE=AH,
∴∠HAE=90°-60°=30°,
∴∠AEH=
| 1 |
| 2 |
∴∠HED=75°-45°=30°.
点评:本题考查了矩形的性质、等边三角形的判定与性质以及等腰三角形的判定与性质;证明三角形是等腰三角形和等边三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,分别以直角三角形ABC的三边作正三角形,已知AC=6,AB=10,阴影部分的面积分别记为S1,S2,S3,则S1+S3-S2的值为( )
如图,分别以直角三角形ABC的三边作正三角形,已知AC=6,AB=10,阴影部分的面积分别记为S1,S2,S3,则S1+S3-S2的值为( )| A、24 | ||
| B、48 | ||
C、25
| ||
D、50
|
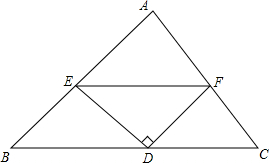 如图,已知△ABC中,D是BC的中点,ED⊥DF.求证:BE+CF>EF.
如图,已知△ABC中,D是BC的中点,ED⊥DF.求证:BE+CF>EF. 在△ABC中,AB=AC,点D是直线BC上一点(不与点B、C重合)以AD为一边,在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
在△ABC中,AB=AC,点D是直线BC上一点(不与点B、C重合)以AD为一边,在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.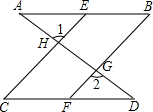 如图,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,如果∠1=∠2,∠B=∠C,试说明∠A=∠D,并写出每一步推理的依据.
如图,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,如果∠1=∠2,∠B=∠C,试说明∠A=∠D,并写出每一步推理的依据.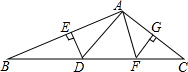 如图,△ABC中,∠BAC=100°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
如图,△ABC中,∠BAC=100°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足. 如图,点A、C、D、F在同一条直线上,AB=FE,BC=ED,AD=FC.∠B与∠E相等吗?为什么?
如图,点A、C、D、F在同一条直线上,AB=FE,BC=ED,AD=FC.∠B与∠E相等吗?为什么? 如图所示,BC平分∠ABO交y轴正半轴于C点,AB=m,S△ABC=m.则点C的坐标为
如图所示,BC平分∠ABO交y轴正半轴于C点,AB=m,S△ABC=m.则点C的坐标为