题目内容
8．
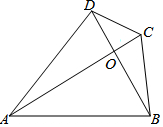如图，在Rt△ABO中，∠AOB=90°，AO+BO=5，延长AO到C，使OC=3，延长BO到D，使OD=4，连接BC、CD、DA，则四边形ABCD面积的最大值为18．
分析 设AO=x，则BO=5-x，得到AC=x+3，BD=9-x，得到二次函数的解析式，于是得到结论．
解答 解：设AO=x，则BO=5-x，
∵OC=3，OD=4，
∴AC=x+3，BD=9-x，
∴S四边形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$（x+3）（9-x）=-$\frac{1}{2}$x2+3x+$\frac{27}{2}$=-$\frac{1}{2}$（x-3）2+18，
∴当x=3时，四边形ABCD的面积有最大值为18，
即四边形ABCD面积的最大值为18，
故答案为：18．
点评 本题考查了二次函数的最值，四边形的面积的计算，能根据题意列出函数关系式是解题的关键．
练习册系列答案
相关题目
19．下列关于圆的切线的说法正确的是（ ）
| A． | 垂直于圆的半径的直线是圆的切线 | |
| B． | 与圆只有一个公共点的射线是圆的切线 | |
| C． | 经过半径的一端且垂直于半径的直线是圆的切线 | |
| D． | 如果圆心到一条直线的距离等于半径长，那么这条直线是圆的切线 |
根据老师在如图所示的背板上给出的内容，完成下列各小题．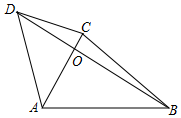
如图，点O是四边形ABCD对角线AC、BD的交点，∠BAD与∠ACB互补，$\frac{OD}{OB}$=$\frac{3}{5}$，AD=6，AB=7，AC=5，则BC的长为$\frac{50}{7}$．
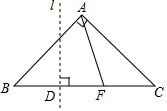如图，等腰Rt△ABC中，AB=AC=1，点F是边BC上不与点B、C重合的一个动点，直线l垂直平分BF，垂足为D，当△AFC是等腰三角形时，BD的长为$\frac{\sqrt{2}}{4}$或$\frac{\sqrt{2}-1}{2}$．
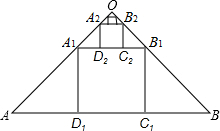如图，等腰直角三角形OAB中，∠AOB=90°，AB=1，在△OAB中作内接正方形A1B1C1D1；在等腰直角三角形OA1B1中，作内接正方形A2B2C2D2；在等腰直角三角形OA2B2中，作内接正方形A3B3C3D3…；依次作下去，则第n个正方形AnBnCnDn的面积是$\frac{1}{{9}^{n}}$．