题目内容
7.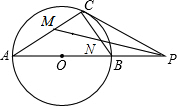 如图,已知⊙O为△ABC的外接圆,AB为⊙O直径,点P为线段AB延长线上一点,连接PC,∠CAB=∠BCP,PM为∠CPB的角平分线,交AC于点M,交BC于点N
如图,已知⊙O为△ABC的外接圆,AB为⊙O直径,点P为线段AB延长线上一点,连接PC,∠CAB=∠BCP,PM为∠CPB的角平分线,交AC于点M,交BC于点N (1)求证:PC为⊙O的切线;
(2)若∠CPB=30°,NC=3时,求MN的长.
分析 (1)连接OC,由AB是直径,得出∠CAB+∠ABC=90°,再由∠OCB=∠ABC,∠CAB=∠BCP,得出∠OCP=90°,即可证出PC为⊙O的切线;
(2)先证明△OBC为等边三角形,得出∠ABC=60°,∠CAB=30°,再由PM为∠CPB的角平分线,得出∠APM=15°,根据外角求出∠CMN=45°,MC=NC=3,根据勾股定理即可求出MN.
解答 (1)证明:连接OC,如图所示: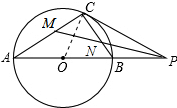 ∵AB是⊙O直径,
∵AB是⊙O直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°,
∵OB=OC,
∴∠OCB=∠ABC,
又∵∠CAB=∠BCP,
∴∠OCB+∠BCP=90°,
即∠OCP=90°,
∴PC⊥OC,
∴PC为⊙O的切线;
(2)解:∵∠CPB=30°,
∴∠COB=60°,
∵OB=OC,
∴△OBC为等边三角形,
∴∠ABC=60°,
∴∠CAB=30°,
∵PM为∠CPB的角平分线,
∴∠APM=15°,
∴∠CMN=30°+15°=45°,
∴△CMN为等腰直角三角形,
∴MC=NC=3,
∴MN=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$.
点评 本题考查了切线的判定、圆周角定理、等边三角形的判定与性质、等腰直角三角形的判定、勾股定理;熟练掌握切线的判定定理,并能进行有关推理计算是解决问题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 如图,△ABC是等边三角形,若点A绕点C顺时针旋转30°至点A′,联结A′B,则∠ABA′度数是15°.
如图,△ABC是等边三角形,若点A绕点C顺时针旋转30°至点A′,联结A′B,则∠ABA′度数是15°. 如图,AB是⊙O的直径,C,D两点在⊙O上,∠BCD=25°,则∠AOD的度数为130°.
如图,AB是⊙O的直径,C,D两点在⊙O上,∠BCD=25°,则∠AOD的度数为130°.