题目内容
5.在△ABC中,AB=$\sqrt{3}$,AC=4,∠A=60°,求S△ABC.分析 此题可以作BD⊥AC.在直角三角形ABD中,可求得∠ABD=30°,所以AD=$\frac{\sqrt{3}}{2}$.再根据勾股定理求得BD=$\frac{3}{2}$,根据三角形的面积公式,即可求得S△ABC=$\frac{1}{2}$×4×$\frac{3}{2}$=3.
解答 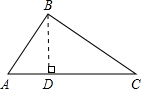 解:过B作BD⊥AC于D.在Rt△ABD中,
解:过B作BD⊥AC于D.在Rt△ABD中,
∵∠A=60°,
∴∠ABD=30°,
又∵AB=$\sqrt{3}$,
∴AD=$\frac{\sqrt{3}}{2}$,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\frac{3}{2}$,
∵AC=4,
∴S△ABC=$\frac{1}{2}$AC•BD=$\frac{1}{2}×4×\frac{3}{2}$=3.
点评 本题考查了解直角三角形,构造出直角三角形,充分利用边角关系是解题的关键.

练习册系列答案
相关题目
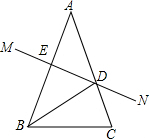 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AC于点D,交AB于E.
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AC于点D,交AB于E. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=8,tanA=$\frac{3}{4}$,求CD的长.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=8,tanA=$\frac{3}{4}$,求CD的长. 如图,△ABC中,sin∠ABC=$\frac{\sqrt{21}}{14}$,AB=10,AC=5,求sin∠ACB.
如图,△ABC中,sin∠ABC=$\frac{\sqrt{21}}{14}$,AB=10,AC=5,求sin∠ACB.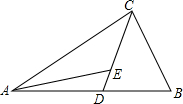 如图,△ABC中,点D在AB边上,AD=CD,点E在CD上,∠ABC+∠AEC=180°,图中是否存在与BC相等的线段?若存在,请找出,并加以证明,若不存在,请说明理由.
如图,△ABC中,点D在AB边上,AD=CD,点E在CD上,∠ABC+∠AEC=180°,图中是否存在与BC相等的线段?若存在,请找出,并加以证明,若不存在,请说明理由.