题目内容
7.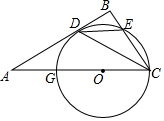 如图,点O为Rt△ABC斜边AC上一点,以点O为圆心,OC长为半径的⊙O与AB相切于点D,分别交AC,BC于点G,E.
如图,点O为Rt△ABC斜边AC上一点,以点O为圆心,OC长为半径的⊙O与AB相切于点D,分别交AC,BC于点G,E.(1)求证:$\widehat{DG}$=$\widehat{DE}$.
(2)若DE∥AC,BE=1,求AG和$\widehat{DG}$的长.
分析 (1)连接OD.首先证明OD∥BC,推出∠ODC=∠DCE,由OD=OC,推出∠ODC=∠OCD,推出∠DCG=∠DCE即可证明;
(2)首先证明四边形ODEC是菱形,推出△OEC是等边三角形即可解决问题;
解答 (1)证明:连接OD.
∵AB是切线,
∴OD⊥AB,
∴∠ADO=∠B=90°,
∴OD∥BC,
∴∠ODC=∠DCE,
∵OD=OC,
∴∠ODC=∠OCD,
∴∠DCG=∠DCE,
∴$\widehat{DG}$=$\widehat{DE}$.
(2)连接OE.
∵DE∥OC,DO∥EC,
∴四边形ODEC是平行四边形,
∵OD=OC,
∴四边形ODEC是菱形,
∴OC=CE=OE,
∴△OEC是等边三角形,
∴∠BCA=60°,∠BDE=∠A=30°,
∵BE=1,
∴DE=OD=OC=EC=2BE=2,
∴BC=3,
∴AC=2BC=6,
∴AG=AC-CG=2,
$\widehat{DG}$的长=$\frac{60π•2}{180}$=$\frac{2}{3}$π.
点评 本题考查切线的性质、平行线的性质、菱形的判定和性质、等边三角形的判定和性质、解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
18.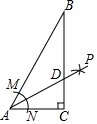 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,小于AC为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP交BC于点,则下列说法不正确的是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,小于AC为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP交BC于点,则下列说法不正确的是( )
 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,小于AC为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP交BC于点,则下列说法不正确的是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,小于AC为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP交BC于点,则下列说法不正确的是( )| A. | AD平分∠BAC | B. | S△DAC:S△ABC=1:2 | ||
| C. | 点D在线段AB的垂直平分线上 | D. | ∠ADC=60° |
2. 如图是一组不等式组的解集在数轴上的表示,则该不等式组的解集为( )
如图是一组不等式组的解集在数轴上的表示,则该不等式组的解集为( )
 如图是一组不等式组的解集在数轴上的表示,则该不等式组的解集为( )
如图是一组不等式组的解集在数轴上的表示,则该不等式组的解集为( )| A. | -1<x≤2 | B. | x≤2 | C. | -1≤x<2 | D. | x>-1 |
16.下列各图中,∠1与∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
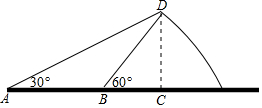 如图,由山脚下的一点A测得山顶D的仰角是30°,从A前进100米到B,再次测得山顶D的仰角为60°,求山高CD的高度(结果精确到0.1米).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,由山脚下的一点A测得山顶D的仰角是30°,从A前进100米到B,再次测得山顶D的仰角为60°,求山高CD的高度(结果精确到0.1米).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)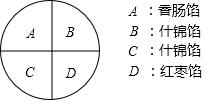 大年夜吃饺子是中华民族的传统习俗,妈妈为洋洋准备了四只饺子:一只香肠陷A,两只什锦馅B和C,一只红枣馅D,四只饺子除内部馅料不同外,其他均一切相同,洋洋喜欢吃什锦馅的饺子.
大年夜吃饺子是中华民族的传统习俗,妈妈为洋洋准备了四只饺子:一只香肠陷A,两只什锦馅B和C,一只红枣馅D,四只饺子除内部馅料不同外,其他均一切相同,洋洋喜欢吃什锦馅的饺子.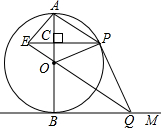 如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.
如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.