题目内容
 如图,在半径为
如图,在半径为| 5 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
考点:垂径定理,勾股定理
专题:计算题
分析:作OE⊥AB于E,OF⊥CD于F,连结OD、OB,如图,根据垂径定理得到AE=BE=
AB=2,DF=CF=
CD=2,根据勾股定理在Rt△OBE中计算出OE=1,同理可得OF=1,接着证明四边形OEPF为正方形,于是得到OP=
OE=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
解答: 解:作OE⊥AB于E,OF⊥CD于F,连结OD、OB,如图,
解:作OE⊥AB于E,OF⊥CD于F,连结OD、OB,如图,
则AE=BE=
AB=2,DF=CF=
CD=2,
在Rt△OBE中,∵OB=
,BE=2,
∴OE=
=1,
同理可得OF=1,
∵AB⊥CD,
∴四边形OEPF为矩形,
而OE=OF=1,
∴四边形OEPF为正方形,
∴OP=
OE=
.
故选B.
 解:作OE⊥AB于E,OF⊥CD于F,连结OD、OB,如图,
解:作OE⊥AB于E,OF⊥CD于F,连结OD、OB,如图,则AE=BE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OBE中,∵OB=
| 5 |
∴OE=
| OB2-BE2 |
同理可得OF=1,
∵AB⊥CD,
∴四边形OEPF为矩形,
而OE=OF=1,
∴四边形OEPF为正方形,
∴OP=
| 2 |
| 2 |
故选B.
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,若∠B=100°,那么∠A、∠D的度数分别是( )度.
如图,在平行四边形ABCD中,若∠B=100°,那么∠A、∠D的度数分别是( )度.| A、80、100 |
| B、100、80 |
| C、80、80 |
| D、100、100 |
如图是正方体的展开图的有( )个.


| A、2个 | B、3个 | C、4个 | D、5个 |
 如图所示,∠1+∠2+∠3+∠4等于
如图所示,∠1+∠2+∠3+∠4等于 如图所示,15只空油桶堆在一起,每只油桶的底面直径均为50厘米.现在要给它们盖一个遮雨棚,遮雨棚起码要多高?(结果精确到0.01厘米)
如图所示,15只空油桶堆在一起,每只油桶的底面直径均为50厘米.现在要给它们盖一个遮雨棚,遮雨棚起码要多高?(结果精确到0.01厘米) 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上. 如图,以数轴的单位长线段和单位长线段的两倍为边作一个长方形,以数轴的原点为圆心、长方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是( )
如图,以数轴的单位长线段和单位长线段的两倍为边作一个长方形,以数轴的原点为圆心、长方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是( )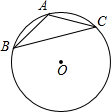 等腰△ABC的顶角∠A=120°,腰AB=AC=10,△ABC的外接圆半径等于
等腰△ABC的顶角∠A=120°,腰AB=AC=10,△ABC的外接圆半径等于