题目内容
 等腰△ABC的顶角∠A=120°,腰AB=AC=10,△ABC的外接圆半径等于
等腰△ABC的顶角∠A=120°,腰AB=AC=10,△ABC的外接圆半径等于考点:圆周角定理,等边三角形的判定与性质
专题:
分析:过点A作AD⊥BC于点D,连接CO并延长交⊙O于点E,连接BE,先根据等腰三角形的性质求出∠ABC的度数,故可得出BD及BC的长,由圆周角定理可知∠CBE=90°,再由圆内接四边形的性质IQUC胡∠E的度数,根据锐角三角函数的定义即可得出结论.
解答: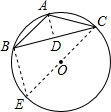 解:过点A作AD⊥BC于点D,连接CO并延长交⊙O于点E,连接BE,
解:过点A作AD⊥BC于点D,连接CO并延长交⊙O于点E,连接BE,
∵等腰△ABC的顶角∠A=120°,腰AB=AC=10,
∴∠ABC=∠ACB=
=30°,
∴BD=AB•cos30°=10×
=5
,
∴BC=2BD=10
.
∵CE是⊙O的直径,
∴∠CBE=90°.
∵四边形ABEC是圆内接四边形,
∴∠E=180°-∠BAC=180°-120°=60°,
∴CE=
=
=20,
∴OC=
CE=10.
故答案为:10.
 解:过点A作AD⊥BC于点D,连接CO并延长交⊙O于点E,连接BE,
解:过点A作AD⊥BC于点D,连接CO并延长交⊙O于点E,连接BE,∵等腰△ABC的顶角∠A=120°,腰AB=AC=10,
∴∠ABC=∠ACB=
| 180°-120° |
| 2 |
∴BD=AB•cos30°=10×
| ||
| 2 |
| 3 |
∴BC=2BD=10
| 3 |
∵CE是⊙O的直径,
∴∠CBE=90°.
∵四边形ABEC是圆内接四边形,
∴∠E=180°-∠BAC=180°-120°=60°,
∴CE=
| BC |
| sin60° |
10
| ||||
|
∴OC=
| 1 |
| 2 |
故答案为:10.
点评:本题考查的是圆周角定理,熟知直径所对的圆周角是直角是解答此题的关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
下面的四个图案中,既包含图形的旋转,又包含图形的轴对称的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在半径为
如图,在半径为| 5 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
 一只跳蚤在第一象限及x轴,y轴上跳动,在第一秒钟,它从跳点跳动到(0,1),然后继续按图中箭头所示方向跳动即(0,0)→(0,1)→(1,1)→(1,0)→…1,且每秒跳动一个单位.那么第35秒时跳蚤所在位置的坐标是( )
一只跳蚤在第一象限及x轴,y轴上跳动,在第一秒钟,它从跳点跳动到(0,1),然后继续按图中箭头所示方向跳动即(0,0)→(0,1)→(1,1)→(1,0)→…1,且每秒跳动一个单位.那么第35秒时跳蚤所在位置的坐标是( )| A、(5,0) |
| B、(4,0) |
| C、(0,5) |
| D、(5,5) |
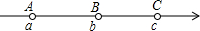 如图,数轴上的A,B,C三点所表示的数是分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )
如图,数轴上的A,B,C三点所表示的数是分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )| A、点A的左边 |
| B、点A与点B之间 |
| C、点B与点C之间 |
| D、点B与点C之间(靠近点C)或点C的右边 |
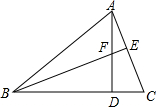 △ABC中,∠C=60°,高BE经过高AD的中点F,EF=1,则BF长为( )
△ABC中,∠C=60°,高BE经过高AD的中点F,EF=1,则BF长为( )| A、2 | B、3 | C、4 | D、5 |
函数值y随x的增大而减小的是( )
| A、y=1+x | ||
B、y=
| ||
| C、y=-x+1 | ||
| D、y=-2+3x |
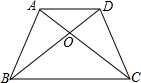 等腰梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,AC=2,∠BOC=120°,求AD+BC的值.
等腰梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,AC=2,∠BOC=120°,求AD+BC的值. 如图,若sinα=
如图,若sinα=