题目内容
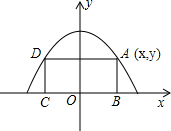 如图,矩形ABCD的顶点B,C在x轴上,A,D在抛物线y=-
如图,矩形ABCD的顶点B,C在x轴上,A,D在抛物线y=-| 1 |
| 2 |
(1)设点A的坐标为(x,y),试求矩形ABCD的周长P关于自变量x的函数关系式,并求自变量x的取值范围.
(2)是否存在这样的矩形ABCD,使它的周长为9?试证明你的结论.
考点:二次函数综合题
专题:综合题
分析:(1)由图及四边形ABCD为矩形可知AD∥x轴,长为2x的绝对值,AB的长为A点的纵坐标,由x与y的关系,可求得p关于自变量x的解析式,由矩形ABCD在抛物线里面,可得x的取值范围.
(2)令P=9,解出x的值后,即可作出判断.
(2)令P=9,解出x的值后,即可作出判断.
解答:解:(1)∵A点在x轴的正方向上坐标为(x,y),四边形ABCD为矩形,BC在x轴上,
∴AD∥x轴,
又∵抛物线关于y轴对称,
∴A、B关于y轴分别与D、C对称,
∴AD的长为2x,AB长为y,
∴周长p=2y+4x=2(-
x2+2)+4x=-x2+4x+4,
∵A在抛物线上,且ABCD组成矩形,
∴0<x<2,
∴p=-x2+4x+4,其中0<x<2.
(2)由题意得:-x2+4x+4=9,
因为方程无解,
故不存在这样的矩形ABCD,使它的周长为9.
∴AD∥x轴,
又∵抛物线关于y轴对称,
∴A、B关于y轴分别与D、C对称,
∴AD的长为2x,AB长为y,
∴周长p=2y+4x=2(-
| 1 |
| 2 |
∵A在抛物线上,且ABCD组成矩形,
∴0<x<2,
∴p=-x2+4x+4,其中0<x<2.
(2)由题意得:-x2+4x+4=9,
因为方程无解,
故不存在这样的矩形ABCD,使它的周长为9.
点评:本题考查了二次函数的综合,解答本题的关键是得出周长P关于x的表达式,难度一般,注意数形结合思想的运用.

练习册系列答案
相关题目
在-2,+3.5,0,-
,-0.7,11中,负分数有( )
| 2 |
| 3 |
| A、l个 | B、2个 | C、3个 | D、4个 |
 一座圆弧形拱桥如图,圆弧形桥拱的跨度AB=12米,C为桥拱的中点,拱高CD=4米,求拱桥的半径.
一座圆弧形拱桥如图,圆弧形桥拱的跨度AB=12米,C为桥拱的中点,拱高CD=4米,求拱桥的半径. 在如图所示的平面直角坐标系中,直线OA的解析式为y=
在如图所示的平面直角坐标系中,直线OA的解析式为y= 如图,在四边形ACDE中,AE⊥AC于A,BF⊥AC于B,CD⊥AC于C,若AE=1.5m,BF=3.2m,AB=3m,BC=9m.求CD的长.
如图,在四边形ACDE中,AE⊥AC于A,BF⊥AC于B,CD⊥AC于C,若AE=1.5m,BF=3.2m,AB=3m,BC=9m.求CD的长. 已知一次函数y=-kx+k的图象如图,则二次函数y=-kx2-2x+k的图象大致是( )
已知一次函数y=-kx+k的图象如图,则二次函数y=-kx2-2x+k的图象大致是( )



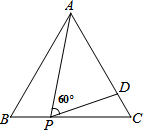 如图,等边三角形△ABC的边长为3,点P为BC上的一点,且PC=2,点D为AC上的一点,若∠APD=60°,则CD的长为
如图,等边三角形△ABC的边长为3,点P为BC上的一点,且PC=2,点D为AC上的一点,若∠APD=60°,则CD的长为