题目内容
18. 如图,线段AC与BD相交于点O,连接AB,CD,若AB∥CD,BO=DO,AF=CE.
如图,线段AC与BD相交于点O,连接AB,CD,若AB∥CD,BO=DO,AF=CE.(1)请说明点O是AC的中点;
(2)猜想BE与DF的数量关系和位置关系,并说明理由.
分析 (1)证△ABO≌△CDO即可;
(2)BE=DF,BE∥DF.证△BEO≌△DFO即可.
解答 (1)证明:∵AB∥CD,
∴∠A=∠C,
在△ABO和△CDO中
$\left\{\begin{array}{l}{∠A=∠C}\\{∠AOB=∠COD}\\{BO=DO}\end{array}\right.$,
∴△ABO≌△CDO,
∴AO=CO,
即点O是AC的中点.
(2)BE=DF,BE∥DF.
理由:∵AF=CE,AO=CO,
∴FO=EO,
在△BOE和△DOF中
$\left\{\begin{array}{l}{EO=FO}\\{∠BOE=∠DOF}\\{BO=DO}\end{array}\right.$,
∴△BOE≌△DOF,
∴BE=DF,∠DFO=∠BEO
∴BE∥DF.
点评 本题考查了全等三角形的判定与性质,熟练地掌握全等三角形的判定方法是解决问题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
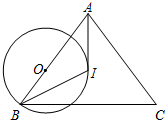 如图,在△ABC中,I是内心,O是AB边上一点,⊙O经过B点且与AI相切于I点.
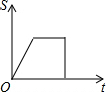
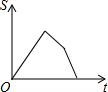
如图,在△ABC中,I是内心,O是AB边上一点,⊙O经过B点且与AI相切于I点. 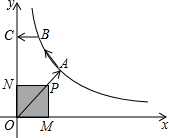 如图,已知A、B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
如图,已知A、B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )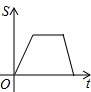
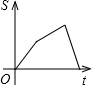
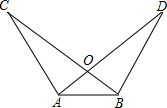 如图,已知AC=BD,∠C=∠D,试说明AD=BC,小丽的说理过程如下:
如图,已知AC=BD,∠C=∠D,试说明AD=BC,小丽的说理过程如下: 任意给一个非零数,按如图程序进打计算,输出结果是m+2.
任意给一个非零数,按如图程序进打计算,输出结果是m+2.