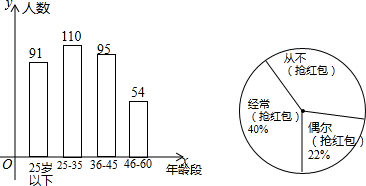
题目内容
3．已知0＜x＜1，且x+$\frac{1}{x}$=$\sqrt{8}$，求x-$\frac{1}{x}$的值．分析 把已知等式两边平方，利用完全平方公式化简，整理求出x2+$\frac{1}{{x}^{2}}$的值，原式平方，利用完全平方公式化简，开方即可求出值．
解答 解：∵0＜x＜1，且x+$\frac{1}{x}$=$\sqrt{8}$，
∴（x+$\frac{1}{x}$）2=x2+$\frac{1}{{x}^{2}}$+2=8，即x2+$\frac{1}{{x}^{2}}$=6，x-$\frac{1}{x}$＜0，
∴（x-$\frac{1}{x}$）2=x2+$\frac{1}{{x}^{2}}$-2=4，
则x-$\frac{1}{x}$=-2．
点评 此题考查了完全平方公式，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
教学练新同步练习系列答案
相关题目
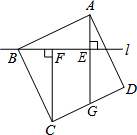如图，过正方形ABCD的顶点B作直线l，过点A，C作直线l的垂线，垂足分别为E，F，直线AE交CD于点G．
如图，线段AC与BD相交于点O，连接AB，CD，若AB∥CD，BO=DO，AF=CE．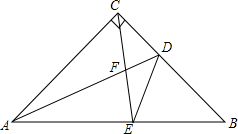
如图，在等腰Rt△ABC中，∠ACB=90°，AC=BC，D为BC的中点，E为斜边AB上一点，且AE=2EB，CE与AD交于点F，连接DE．