题目内容
18.化简:$\frac{\sqrt{2}+1}{\sqrt{2}-1}$=3﹢2$\sqrt{2}$.分析 先找到$\sqrt{2}$-1的有理化因式,再分母有理化即可.
解答 解:$\frac{\sqrt{2}+1}{\sqrt{2}-1}$=$\frac{(\sqrt{2}+1)^{2}}{(\sqrt{2}+1)(\sqrt{2}-1)}$=3﹢2$\sqrt{2}$,
故答案为3﹢2$\sqrt{2}$.
点评 本题考查了二次根式的有理化.根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
8.下列运算正确的是( )
| A. | -3-2=-1 | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | a6÷a3=a3 | D. | (a+b)2=a2+b2 |
6.若代数式$\sqrt{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x<2 | B. | x>2 | C. | x≥2 | D. | x≤2 |
10.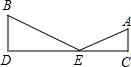 如图,球从A处射击,经过台边挡板CD反击,击中球B;已知AC=10cm,BD=15cm,CD=50cm,则点E距点C的距离是( )
如图,球从A处射击,经过台边挡板CD反击,击中球B;已知AC=10cm,BD=15cm,CD=50cm,则点E距点C的距离是( )
 如图,球从A处射击,经过台边挡板CD反击,击中球B;已知AC=10cm,BD=15cm,CD=50cm,则点E距点C的距离是( )
如图,球从A处射击,经过台边挡板CD反击,击中球B;已知AC=10cm,BD=15cm,CD=50cm,则点E距点C的距离是( )| A. | 20cm | B. | 30cm | C. | 15cm | D. | 35cm |
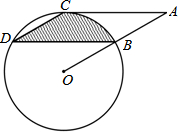 如图,点B,C,D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,BD=4$\sqrt{3}$,则由弦CD,BD与弧BC所围成的阴影部分的面积是$\frac{8}{3}$π.(结果保留π)
如图,点B,C,D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,BD=4$\sqrt{3}$,则由弦CD,BD与弧BC所围成的阴影部分的面积是$\frac{8}{3}$π.(结果保留π)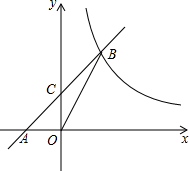 已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连结BO,若S△AOB=4.
已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连结BO,若S△AOB=4. 如图是由6个相同的小立方块搭成的几何体,这个几何体的左视图是( )
如图是由6个相同的小立方块搭成的几何体,这个几何体的左视图是( )


