题目内容
17.第一盒乒乓球中有3个白球,1个黄球,第二盒乒乓球中有2个白球,2个黄球,分别从每个盒子中随机地取出1个球,则取出的两个球中有一个白球一个黄球的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与取出的两个球中有一个白球一个黄球的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有16种等可能的结果,取出的两个球中有一个白球一个黄球的有8种情况,
∴取出的两个球中有一个白球一个黄球的概率是:$\frac{8}{16}$=$\frac{1}{2}$.
故选A.
点评 此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
8.下列运算正确的是( )
| A. | -3-2=-1 | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | a6÷a3=a3 | D. | (a+b)2=a2+b2 |
6.若代数式$\sqrt{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x<2 | B. | x>2 | C. | x≥2 | D. | x≤2 |




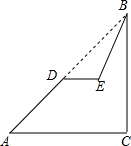 如图,已知斜坡AB长为60$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC.现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE,若修建的斜坡BE的坡比为$\sqrt{3}$:1,求休闲平台DE的长是多少米?(结果保留根号).
如图,已知斜坡AB长为60$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC.现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE,若修建的斜坡BE的坡比为$\sqrt{3}$:1,求休闲平台DE的长是多少米?(结果保留根号).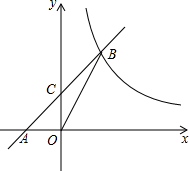 已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连结BO,若S△AOB=4.
已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连结BO,若S△AOB=4.