题目内容
3. 如图,已知∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC且∠1=∠2
如图,已知∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC且∠1=∠2求证:∠A=∠C
将下面证明过程补充完整,并在括号内填写理由.
证明:∵BE、DF分别平分∠ABC、∠ADC(已知)
∴∠1═$\frac{1}{2}$∠ABC,∠3=$\frac{1}{2}$∠ADC (角平分线的定义)
∵∠ADC=∠ABC
∴∠1=∠3 (等量代换)
∵∠1=∠2(已知)
∴∠2=∠3 (等量代换)
∴AB∥CD(内错角相等,两直线平行)
∴∠A+∠ADC=180°,∠C+∠ABC=180° (两直线平行,同旁内角互补)
∴∠A=∠C( 等量代换)
分析 根据角平分线的定义以及平行线的性质,即可得到∠ABC=∠ADC,根据平行线的判定与性质,依据等角的补角相等即可证得.
解答 证明:∵BE、DF分别平分∠ABC、∠ADC(已知)
∴∠1=$\frac{1}{2}$∠ABC,∠3=$\frac{1}{2}$∠ADC(角平分线的定义)
∵∠ABC=∠ADC(已知)
∴∠1=∠3(等量代换)
∵∠1=∠2(已知)
∴∠2=∠3(等量代换)
∴AB∥CD(内错角相等,两直线平行)
∴∠A+∠ADC=180°,∠C+∠ABC=180°(两直线平行,同旁内角互补)
∴∠A=∠C(等量代换).
故答案为:角平分线的定义,等量代换,等量代换,AB,CD,内错角相等,两直线平行,∠ADC,∠ABC,两直线平行,同旁内角互补.
点评 本题考查了角平分线的定义,以及平行线的判定与性质,补角的性质,同角的补角相等.解题时注意:内错角相等,两直线平行;两直线平行,同旁内角互补.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.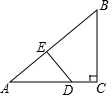 如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )
如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )
 如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )
如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )| A. | ∠A和∠B互为余角 | B. | ∠A和∠ADE互为余角 | ||
| C. | ∠B和∠EDC互为补角 | D. | ∠B和∠DEB互为补角 |
 如图,△ABC的周长为21cm,边AC的垂直平分线为DE交BC于点D,E为垂足,AE=3cm,则△ABD的周长是15cm.
如图,△ABC的周长为21cm,边AC的垂直平分线为DE交BC于点D,E为垂足,AE=3cm,则△ABD的周长是15cm.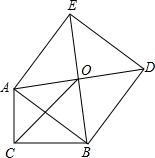 如图,Rt△ABC中,C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点D,连接OC,已知AC=5,OC=6,则另一直角边BC的长为6$\sqrt{2}$-5.
如图,Rt△ABC中,C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点D,连接OC,已知AC=5,OC=6,则另一直角边BC的长为6$\sqrt{2}$-5.