题目内容
一个不透明的盒子里装有分别标上2008、-
、-π、0、tan45°、1.75、2、-
共8个数字卡片,小明从中任意抽取一张,并用其上所标的数代替m的值,使关于x的方程(m-2)x2+x-1=0有实数根的概率是多少?
| 9 |
| 7 |
| 3 |
考点:概率公式,根的判别式
专题:
分析:首先求出能够使关于x的方程(m-2)x2+x-1=0有实数根的m的取值范围,然后在这8张卡片中挑选出满足条件的数,让满足条件的数的个数除以数的总数即为所求.
解答:解:当m-2=0,即m=2时,方程为x-1=0,是一元一次方程,一定有实数根;
当m-2≠0,即m≠2时,方程为(m-2)x2+x-1=0,是一元二次方程,△=1-4(m-2)(-1)≥0,即m≥
时,方程有实数根;
综上可知m≥
时,方程有实数根.
∵在2008、-
、-π、0、tan45°、1.75、2、-
8个数中,不小于
的数有1.75,2和2008共3个数,
∴小明从中任意抽出一张,并用其上所标的数代替m的值,那么这个值恰好能使关于x的方程(m-2)x2+x-1=0有实数根的概率是
.
当m-2≠0,即m≠2时,方程为(m-2)x2+x-1=0,是一元二次方程,△=1-4(m-2)(-1)≥0,即m≥
| 7 |
| 4 |
综上可知m≥
| 7 |
| 4 |
∵在2008、-
| 9 |
| 7 |
| 3 |
| 7 |
| 4 |
∴小明从中任意抽出一张,并用其上所标的数代替m的值,那么这个值恰好能使关于x的方程(m-2)x2+x-1=0有实数根的概率是
| 3 |
| 8 |
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
,得出m的取值范围是解题的关键.
| m |
| n |

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
袋中共有3个红球,3个白球,它们只有颜色上的区别,随机地摸一个后不放回,再随机摸一个,则第一次摸到红球,并且第二次摸到白球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知线段AB两端的坐标A(4,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的
后得到线段CD,A点的对应点为C点,则端点C的坐标为( )
| 1 |
| 2 |
| A、(2,3) |
| B、(2,1) |
| C、(4,3) |
| D、(4,1) |
 如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB,连接AF,BF.
如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB,连接AF,BF.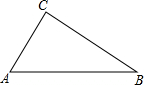 如图,△ABC,AB=5,BC=4,AC=3.
如图,△ABC,AB=5,BC=4,AC=3.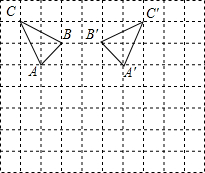 在如图所示的网格(每个小正方形的边长为1)中,△ABC的顶点A的坐标为(-2,1).
在如图所示的网格(每个小正方形的边长为1)中,△ABC的顶点A的坐标为(-2,1).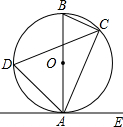 如图,已知AB是⊙O的直径,点C、D在⊙O的上,点E在⊙O的外,∠EAC=∠D=60°.
如图,已知AB是⊙O的直径,点C、D在⊙O的上,点E在⊙O的外,∠EAC=∠D=60°.