题目内容
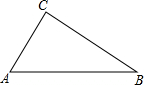 如图,△ABC,AB=5,BC=4,AC=3.
如图,△ABC,AB=5,BC=4,AC=3.(1)用直尺和圆规作边AB的垂直平分线MN;
(2)在直线MN上找一点D,使△ADC周长最小,并写出△ADC最小周长是
考点:轴对称-最短路线问题,作图—基本作图
专题:
分析:(1)分别以点A、B为圆心,以大于
AB长度为半径画弧,在AB的两边分别相交于点M、N,作直线MN即可;
(2)根据轴对称确定最短路线问题,点D为MN与BC的交点,根据线段垂直平分线上的点到两端点的距离相等可得AD=BD,然后求出△ADC最小周长=AC+BC,然后计算即可得解.
| 1 |
| 2 |
(2)根据轴对称确定最短路线问题,点D为MN与BC的交点,根据线段垂直平分线上的点到两端点的距离相等可得AD=BD,然后求出△ADC最小周长=AC+BC,然后计算即可得解.
解答: 解:(1)边AB的垂直平分线MN如图所示;
解:(1)边AB的垂直平分线MN如图所示;
(2)由轴对称确定最短路线问题,点D为MN与BC的交点,
∵MN垂直平分AB,
∴AD=BD,
∴△ADC最小周长=AC+BC=3+4=7.
故答案为:7.
 解:(1)边AB的垂直平分线MN如图所示;
解:(1)边AB的垂直平分线MN如图所示;(2)由轴对称确定最短路线问题,点D为MN与BC的交点,
∵MN垂直平分AB,
∴AD=BD,
∴△ADC最小周长=AC+BC=3+4=7.
故答案为:7.
点评:本题考查了轴对称确定最短路线问题,线段垂直平分线上的作法,熟记最短路径的确定方法是解题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
下列各式中结果为负数的是( )
| A、-(-3) | ||
| B、(-3)2 | ||
| C、-|-3| | ||
D、
|
 已知一个圆锥体的三视图如图所示,则这个圆锥的侧面积为
已知一个圆锥体的三视图如图所示,则这个圆锥的侧面积为