题目内容
9.将抛物线y=x2+bx+c沿直角坐标平面先向左平移3个单位.再向上平移4个单位.得到了抛物线y=x2 -4x+4(1)请你确定b、c的值;
(2)请你求出抛物线y=x2+bx+c的顶点坐标及对称轴.
分析 (1)根据配方法求出抛物线y=2x2-4x+3的顶点坐标,再利用平移得出原函数的对称轴和顶点坐标,进而得出b,c的值即可;
(2)利用(1)中所求得出顶点坐标和对称轴即可.
解答 解:(1)∵y=x2 -4x+4=(x-2)2.
∴向右平移3个单位.再向下平移4个单位,得到抛物线y=(x-5)2-4.
∴y=x2-10x+21.
∴b=-10,c=21.
(2)由y=x2-10x+21=(x-5)2-4,该抛物线的顶点坐标是(5,-4),对称轴为直线x=5.
点评 此题主要考查了配方法求二次函数的顶点坐标和对称轴以及二次函数的平移,熟练掌握配方法是解题关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
14.下列各数中,是无理数的是( )
| A. | $\sqrt{4}$ | B. | $\frac{22}{7}$ | C. | $\root{3}{8}$ | D. | π-1 |
1.下列交换加数的位置的变形中,正确的是( )
| A. | 6+(-5)=(-5)+6 | B. | 6+(-5)=5+(-6) | C. | 6+(-5)=5+6 | D. | 6+(-5)=(-5)+(-6) |
19. 图中的∠α等于( )
图中的∠α等于( )
 图中的∠α等于( )
图中的∠α等于( )| A. | 55° | B. | 45° | C. | 60° | D. | 65° |
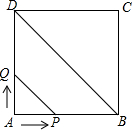 如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C移动.设运动时间为x s,由点P、B、D、Q确定的图形的面积为y cm2,求y与x(0≤x≤8)之间的函数关系式.
如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C移动.设运动时间为x s,由点P、B、D、Q确定的图形的面积为y cm2,求y与x(0≤x≤8)之间的函数关系式.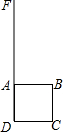 如图,在小路DF的右侧是一片草地,紧靠小路建有一正方形小屋ABCD,现用一根长为6m的牛绳一端系住牛鼻,另一端系在A处.如果小屋的边长为3m,那么这头牛最多能吃掉多大面积的草地?请画出示意图.如果绳长为7m呢?
如图,在小路DF的右侧是一片草地,紧靠小路建有一正方形小屋ABCD,现用一根长为6m的牛绳一端系住牛鼻,另一端系在A处.如果小屋的边长为3m,那么这头牛最多能吃掉多大面积的草地?请画出示意图.如果绳长为7m呢?