题目内容
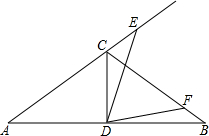 如图,在△ABC中,AC=BC,∠A=30°,D为AB的中点,∠EDF=60°,E,F分别在AC,BC上
如图,在△ABC中,AC=BC,∠A=30°,D为AB的中点,∠EDF=60°,E,F分别在AC,BC上(1)当点E在AC的延长线上时,求
| DE |
| DF |
(2)线段CE、CF、AC存在怎样的数量关系?写出你的猜想并说明理由.
考点:全等三角形的判定与性质,等边三角形的判定与性质,含30度角的直角三角形
专题:
分析:(1)根据等腰三角形的性质,可得CD⊥AB,∠ACD=∠BCD=60°,∠ADC=∠BDC=90°,根据直角三角形的性质,可得DG=
AC=CG,DH=
BC=CH,根据等边三角形的判定,可得△DCG、△DCH是等边三角形,根据全等三角形的判定与性质,可得DE与DF的关系,根据比的意义,可得答案;
(2)根据全等三角形的性质,可得CG与CH的关系,根据等式的性质,可得CE与HF的关系,根据等量代换,可得CF-HF=CF-CE=CH=
BC=
AC,根据等式的性质,可得答案.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据全等三角形的性质,可得CG与CH的关系,根据等式的性质,可得CE与HF的关系,根据等量代换,可得CF-HF=CF-CE=CH=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)如图:

分别取AC、BC的中点G、H,连接DG,DH,
∵△ABC是等腰三角形,∠A=30°,AD是中线,
∴CD⊥AB,∠ACD=∠BCD=60°,∠ADC=∠BDC=90°,
∴DG=
AC=CG,DH=
BC=CH,
∴△DCG、△DCH是等边三角形,
∴DG=DC,∠CDG=∠EDF=∠DCF=60°,
∴∠EDG=∠CDF,
在△DEG和△DFC中,
,
∴△DEG≌△DFC(ASA),
∴GE=CF,DE=DF,即
=1;
(2)∵△DCG、△DCH是等边三角形,DC=DC,
∴△DCG≌△DCH(SSS),
∴CG=CH.
∵EG-CG=CF-CH,
∴CE=HF,
∴CF-HF=CF-CE=CH=
BC=
AC,
∴AC=2(CF-CE).

分别取AC、BC的中点G、H,连接DG,DH,
∵△ABC是等腰三角形,∠A=30°,AD是中线,
∴CD⊥AB,∠ACD=∠BCD=60°,∠ADC=∠BDC=90°,
∴DG=
| 1 |
| 2 |
| 1 |
| 2 |
∴△DCG、△DCH是等边三角形,
∴DG=DC,∠CDG=∠EDF=∠DCF=60°,
∴∠EDG=∠CDF,
在△DEG和△DFC中,
|
∴△DEG≌△DFC(ASA),
∴GE=CF,DE=DF,即
| DE |
| DF |
(2)∵△DCG、△DCH是等边三角形,DC=DC,
∴△DCG≌△DCH(SSS),
∴CG=CH.
∵EG-CG=CF-CH,
∴CE=HF,
∴CF-HF=CF-CE=CH=
| 1 |
| 2 |
| 1 |
| 2 |
∴AC=2(CF-CE).
点评:本题考查了全等三角形的判定与性质,利用了等腰三角形的性质,直角三角形的性质,全等三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(-12)÷〔(-3)+(-15)〕÷(+5)=( )
A、
| ||
B、-
| ||
C、-
| ||
D、
|
下列判断中正确的是( )
| A、全等三角形是面积相等的三角形 |
| B、面积相等的三角形都是全等的三角形 |
| C、等边三角形都是面积相等的三角形 |
| D、面积相等斜边相等的直角三角形都是全等直角三角形 |
 如图所示,边长为5的正方形ABCD的对角线相交于点O,过点O的直线EF分别交AD,BC于点E,F,则阴影部分的面积是
如图所示,边长为5的正方形ABCD的对角线相交于点O,过点O的直线EF分别交AD,BC于点E,F,则阴影部分的面积是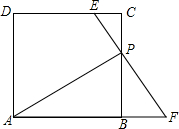 如图,在正方形ABCD中,点P从C点出发,沿射线CB运动,连接AP,过点P作EP⊥AP,分别交直线CD、AB的延长线于点E、F.
如图,在正方形ABCD中,点P从C点出发,沿射线CB运动,连接AP,过点P作EP⊥AP,分别交直线CD、AB的延长线于点E、F. 如图,数轴上的A、B两点分别表示-2、2,在这两点之间,表示有理数的点有多少个?请写出其中3个有理数,并把它们按从小到大的顺序排列.
如图,数轴上的A、B两点分别表示-2、2,在这两点之间,表示有理数的点有多少个?请写出其中3个有理数,并把它们按从小到大的顺序排列. 分析探索题:细心观察如图,认真分析各式,然后解答问题.
分析探索题:细心观察如图,认真分析各式,然后解答问题.