题目内容
10.已知直线过点(1,2)和点(3,0).(1)求这条直线的解析式.
(2)画出函数图象并求出直线与坐标轴围成的三角形的面积.
分析 (1)设直线解析式为y=kx+b,把已知两点坐标代入求出k与b的值,即可确定出解析式;
(2)根据直线解析式求出A与B的坐标,进而确定出OA与OB的长,即可求出直线与坐标轴围成的三角形的面积.
解答  解:(1)设直线解析式为y=kx+b,
解:(1)设直线解析式为y=kx+b,
把(1,2)与(3,0)代入得:$\left\{\begin{array}{l}{k+b=2}\\{3k+b=0}\end{array}\right.$,
解得:k=-1,b=3,
则直线解析式为y=-x+3;
(2)对于直线y=-x+3,
令x=0,得到y=3;令y=0,得到x=3,即A(0,3),B(3,0),
则S△AOB=$\frac{1}{2}$×3×3=$\frac{9}{2}$.
点评 此题考查了待定系数法求一次函数解析式,一次函数的图象,以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图所示,一条数轴被一滩墨迹覆盖了一部分.下列实数中,被墨迹覆盖的是( )
如图所示,一条数轴被一滩墨迹覆盖了一部分.下列实数中,被墨迹覆盖的是( )
 如图所示,一条数轴被一滩墨迹覆盖了一部分.下列实数中,被墨迹覆盖的是( )
如图所示,一条数轴被一滩墨迹覆盖了一部分.下列实数中,被墨迹覆盖的是( )| A. | $-\sqrt{3}$ | B. | $\sqrt{8}$ | C. | $\sqrt{17}$ | D. | $3\frac{1}{2}$ |
15. 如图,是反比例函数y=$\frac{k_1}{x}$与反比例函数y=$\frac{k_2}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若△AOB的面积是1,则k2-k1的值是( )
如图,是反比例函数y=$\frac{k_1}{x}$与反比例函数y=$\frac{k_2}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若△AOB的面积是1,则k2-k1的值是( )
 如图,是反比例函数y=$\frac{k_1}{x}$与反比例函数y=$\frac{k_2}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若△AOB的面积是1,则k2-k1的值是( )
如图,是反比例函数y=$\frac{k_1}{x}$与反比例函数y=$\frac{k_2}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若△AOB的面积是1,则k2-k1的值是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
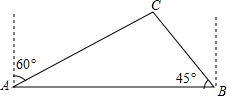 如图,某部门计划在火车站A和大学城B之间修一条长为4公里的公路,经测量在火车站A北偏东60度方向,B西偏北45度方向C处有一圆形公园,要想计划修筑的公路不会穿过公园,则公园半径最大为2($\sqrt{3}$-1)公里.
如图,某部门计划在火车站A和大学城B之间修一条长为4公里的公路,经测量在火车站A北偏东60度方向,B西偏北45度方向C处有一圆形公园,要想计划修筑的公路不会穿过公园,则公园半径最大为2($\sqrt{3}$-1)公里. 如图,DE是AC的垂直平分线,若AE=3cm,△ABD的周长是15cm,则△ABC的周长是21cm.
如图,DE是AC的垂直平分线,若AE=3cm,△ABD的周长是15cm,则△ABC的周长是21cm.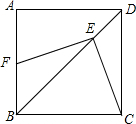 如图,在正方形ABCD中,E是对角线BD上一点,过点E作EF⊥CE,交AB于点F,BF=2,BC=6,则EF=2$\sqrt{5}$.
如图,在正方形ABCD中,E是对角线BD上一点,过点E作EF⊥CE,交AB于点F,BF=2,BC=6,则EF=2$\sqrt{5}$.