题目内容
18．
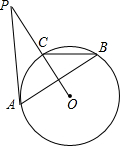如图，PA与⊙O相切，切点为A，PO交⊙O于点C，点B是优弧$\widehat{CBA}$上一点，若∠ABC=32°，则∠P=（ ）度．| A． | 16 | B． | 26 | C． | 36 | D． | 46 |
分析 连接OA，如图，先根据圆周角定理得到∠AOC=2∠ABC=64°，再根据切线的性质得∠OAB=90°，然后利用互余计算∠P的度数．
解答 解：
连接OA，如图，
∵∠ABC=32°，
∴∠AOC=2∠ABC=64°，
∵PA与⊙O相切，
∴OA⊥AB，
∴∠OAB=90°，
∴∠P=90°-∠AOB=90°-64°=26°．
故选B．
点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．
练习册系列答案
相关题目
9．某市四月份连续五天的日最高气温分别为23、20、20、21、26（单位：℃），这组数据的中位数和众数分别是（ ）
| A． | 21℃，20℃ | B． | 21℃，26℃ | C． | 22℃，20℃ | D． | 22℃，26℃ |
6．
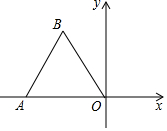如图，点O为平面直角坐标系的原点，点A在x轴上，△OAB是边长为2的等边三角形，以O为旋转中心，将△OAB按顺时针方向旋转60°，得到△OA′B′，那么点A′的坐标为（ ）
如图，点O为平面直角坐标系的原点，点A在x轴上，△OAB是边长为2的等边三角形，以O为旋转中心，将△OAB按顺时针方向旋转60°，得到△OA′B′，那么点A′的坐标为（ ）| A． | （1，$\sqrt{3}$） | B． | （-1，2） | C． | （-1，$\sqrt{2}$） | D． | （-1，$\sqrt{3}$） |
13．若点A（-5，y1），B（1，y2），C（2，y3）在反比例函数y=$\frac{-{a}^{2}-1}{x}$（a为常数）的图象上，则y1，y2，y3的大小关系是（ ）
| A． | y1＜y2＜y3 | B． | y1＜y3＜y2 | C． | y3＜y2＜y1 | D． | y2＜y1＜y3 |
3．已知四边形ABCD是平行四边形，对角线AC与BD相交于点O，那么下列结论中正确的是（ ）
| A． | 当AB=BC时，四边形ABCD是矩形 | B． | 当AC⊥BD时，四边形ABCD是矩形 | ||
| C． | 当OA=OB时，四边形ABCD是矩形 | D． | 当∠ABD=∠CBD时，四边形ABCD是矩形 |
10．要判断一个学生的数学考试成绩是否稳定，那么需要知道他最近连续几次数学考试成绩的（ ）
| A． | 方差 | B． | 平均数 | C． | 中位数 | D． | 众数 |
7．
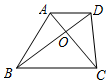如图，在梯形ABCD中，AD∥BC，对角线AC与BD相交于点O，如果AO：AC=2：5，那么S△AOD：S△BOC为（ ）
如图，在梯形ABCD中，AD∥BC，对角线AC与BD相交于点O，如果AO：AC=2：5，那么S△AOD：S△BOC为（ ）| A． | 4：25 | B． | 4：9 | C． | 2：5 | D． | 2：3 |