题目内容

19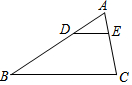．如图，在△ABC中，点D，E分别在AB，AC上，且$\frac{AD}{BD}=\frac{AE}{EC}=\frac{1}{2}$，则S△ADE：S△ABC（　　）
A．1：2B．1：4C．1：8D．1：9

分析 根据已知条件可证明△ADE∽△ABC，利用相似三角形的性质即可得到△ADE与△ABC的面积之比．

解答 解：∵AD：DB=AE：EC=1：2，
∴AD：AB=AE：AC=1：3，
∴∠A=∠A，
∴△ADE∽△ABC，
∴△ADE与△ABC的面积之比=1：9，
故选D．

点评 本题考查了相似三角形的判定和性质，从相似求两个三角形的相似比到面积比而求得．

练习册系列答案
相关题目
9．某市四月份连续五天的日最高气温分别为23、20、20、21、26（单位：℃），这组数据的中位数和众数分别是（　　）
A．21℃，20℃B．21℃，26℃C．22℃，20℃D．22℃，26℃
10．要判断一个学生的数学考试成绩是否稳定，那么需要知道他最近连续几次数学考试成绩的（　　）
A．方差B．平均数C．中位数D．众数
7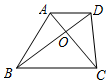．如图，在梯形ABCD中，AD∥BC，对角线AC与BD相交于点O，如果AO：AC=2：5，那么S△AOD：S△BOC为（　　）
A．4：25B．4：9C．2：5D．2：3
14．我国自主研制的世界首颗空间量子科学实验卫星“墨子号”，圆满完成4个月的在轨测试任务后，于2017年1月18日正式交付用户单位使用．在试验期间的某周，“墨子号”向地面接收站发送的信息量如下表：
时间周一周二周三周四周五周六周日
信息量（MB）202210200202200198202
这七天发送的信息量的众数是（　　）
A．198B．200C．202D．210
4．下列运算正确的是（　　）
A．3a•2b=5abB．（-3）-2=-9C．（3.14-π）0=0D．$\sqrt{8}+\sqrt{2}=3\sqrt{2}$
11．函数y=$\frac{1}{\sqrt{4-x}}$中自变量x的取值范围是（　　）
A．x＜4B．x≠4C．x＞4D．x≤4
8．若方程组 $\left\{\begin{array}{l}x+y=a\\ x-y=4a\end{array}\right.$的解是二元一次方程3x-5y-90=0的一个解，则a的值是（　　）
A．4B．5C．6D．7
9．下列调查中，最适合采用全面调查（普查）方式的是（　　）
A．为了解2017年春节联欢晚会收视情况
B．为了解全国中学生的视力状况
C．乘坐高铁时，检查旅客行李是否携带有违禁物品
D．为了解2017年春节中国人最喜欢的过年方式

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网