题目内容
 已知,在△ABC中,AD为∠BAC的平分线,点E在BC的延长线上,且∠EAC=∠B,以DE为直径的半圆交AD于点F,交AE于点M.
已知,在△ABC中,AD为∠BAC的平分线,点E在BC的延长线上,且∠EAC=∠B,以DE为直径的半圆交AD于点F,交AE于点M.(1)判断AF与DF的数量关系,并说明理由;
(2)只用无刻度的直尺画出△ADE的边DE上的高AH;
(3)若EF=4,DF=3,求DH的长.
考点:相似三角形的判定与性质,勾股定理,圆周角定理,作图—复杂作图
专题:
分析:(1)AF=DF,理由是,求AE=DE,根据等腰三角形的性质求出即可;
(2)根据锐角三角形的三条高交于一点画出即可;
(3)证△ADH∽△EDF,得出比例式,代入求出即可.
(2)根据锐角三角形的三条高交于一点画出即可;
(3)证△ADH∽△EDF,得出比例式,代入求出即可.
解答:解:(1)AF=DF,
理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵∠B=∠CAE,
∴∠BAD+∠B=∠CAD+∠CAE.
即∠ADE=∠DAE,
∴AE=DE,
∵DE是直径,
∴EF⊥AD,
∴AF=DF;
(2)如图:连接DM,DM交EF于G,作射线AG交DE于H,此时AH是高.
(3)由勾股定理得:AE=DE=5,
∵∠ADH=∠EDF,∠AHD=∠DFE=90°,
∴△ADH∽△EDF,
∴
=
,
∴
=
,
∴DH=3.6.
理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵∠B=∠CAE,
∴∠BAD+∠B=∠CAD+∠CAE.
即∠ADE=∠DAE,
∴AE=DE,
∵DE是直径,
∴EF⊥AD,
∴AF=DF;
(2)如图:连接DM,DM交EF于G,作射线AG交DE于H,此时AH是高.

(3)由勾股定理得:AE=DE=5,
∵∠ADH=∠EDF,∠AHD=∠DFE=90°,
∴△ADH∽△EDF,
∴
| DH |
| DF |
| AD |
| DE |
∴
| DH |
| 3 |
| 6 |
| 5 |
∴DH=3.6.
点评:本题考查了三角形外角性质,等腰三角形的性质和判定,相似三角形的性质和判定的应用,题目比较好,难度适中.

练习册系列答案
相关题目
用长8米的铝材制成一个矩形窗框,使它的面积为5平方米.若设它的一边长为x米,根据题意列出关于x的方程为( )
| A、x(8-x)=5 |
| B、x(4+x)=5 |
| C、x(4-x)=5 |
| D、x(8-2x)=5 |
 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.若∠1=20°,则∠2的度数是( )
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.若∠1=20°,则∠2的度数是( )| A、20° | B、25° |
| C、65° | D、60° |
 如图,在平面直角坐标系中,矩形纸片ABCD的顶点坐标是A(0,0),C(6,4),E(5,0).将矩形纸片沿直线l折叠,设A′是点A落在矩形CD边上的对应点,点A′的横坐标为2.直线l与x轴、y轴的交点分别为E、F.
如图,在平面直角坐标系中,矩形纸片ABCD的顶点坐标是A(0,0),C(6,4),E(5,0).将矩形纸片沿直线l折叠,设A′是点A落在矩形CD边上的对应点,点A′的横坐标为2.直线l与x轴、y轴的交点分别为E、F. 如图,在8×8的正方形网格中,△ABC的顶点在格点上,点B在x轴上.
如图,在8×8的正方形网格中,△ABC的顶点在格点上,点B在x轴上. 如图,在坐标系中,菱形ABCD的边BC与x轴重合,点B与原点重合,AB=10,∠ABC=60°.动点P从点B出发沿BC边以每秒1个单位长的速度匀速运动;动点Q从点D出发沿折线DC-CB-BA以每秒3个单位长的速度匀速运动,过点P作PF⊥BC,交折线AB-AC于点E,交直线AD于点F.若P、Q两点同时出发,当其中一点到达终点时整个运动随之停止,设运动时间为t秒.
如图,在坐标系中,菱形ABCD的边BC与x轴重合,点B与原点重合,AB=10,∠ABC=60°.动点P从点B出发沿BC边以每秒1个单位长的速度匀速运动;动点Q从点D出发沿折线DC-CB-BA以每秒3个单位长的速度匀速运动,过点P作PF⊥BC,交折线AB-AC于点E,交直线AD于点F.若P、Q两点同时出发,当其中一点到达终点时整个运动随之停止,设运动时间为t秒.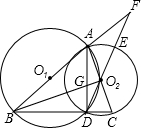 如图,点O2是⊙O1上一点,⊙O2与⊙O1相交于A、D两点,BC⊥AD于D,分别交⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA的延长线于F,BO2交AD于G,连AC.
如图,点O2是⊙O1上一点,⊙O2与⊙O1相交于A、D两点,BC⊥AD于D,分别交⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA的延长线于F,BO2交AD于G,连AC.