题目内容
14．若关于x的一元二次方程4x2-3ax-2a-6=0的常数项为4，则一次项系数为15．分析 根据常数项，可得a的值，根据a的值，可得一次项的系数．
解答 解：由关于x的一元二次方程4x2-3ax-2a-6=0的常数项为4，得
-2a-6=4．
解得a=-5．
一次项系数为-3a=-3×（-5）=15，
故答案为：15．
点评 一元二次方程的一般形式是：ax2+bx+c=0（a，b，c是常数且a≠0）特别要注意a≠0的条件．这是在做题过程中容易忽视的知识点．在一般形式中ax2叫二次项，bx叫一次项，c是常数项．其中a，b，c分别叫二次项系数，一次项系数，常数项．
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
4．已知$\frac{a}{2}=\frac{b}{3}=\frac{c}{4}$≠0，则$\frac{a-b}{c}$的值为（ ）
| A． | $\frac{1}{4}$ | B． | -$\frac{1}{4}$ | C． | 2 | D． | $\frac{1}{2}$ |
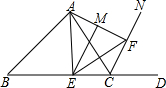如图，△ABC中，∠ACB=60°，点D在射线BC上，CN平分∠ACD，点F为CN上任意一点，连接AF，M为AF中点，过点M作EM⊥AF交BC于点E，连接AE、FE，探究∠EAC与∠EFC之间的数量关系．
19．数轴上的点A表示-3，将点A先向右移动7个单位长度，再向左移动5个单位长度，那么终点到原点的距离是（ ）
| A． | 2个单位长度 | B． | 1个单位长度 | C． | 3个单位长度 | D． | 6个单位长度 |
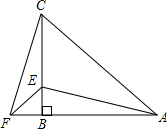如图，△ABC中，AB=BC，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．