题目内容
11.解方程(1)3x2-4=23
(2)4(2-x)2=9
(3)$\left\{\begin{array}{l}x-y=7\\ 3x+2y=16\end{array}\right.$
(4)$\left\{\begin{array}{l}{3(x-1)=y+5}\\{5(y-1)=3(x+5)}\end{array}\right.$.
分析 (1)利用直接开平方法解方程;
(2)利用直接开平方法解方程;
(3)利用加减消元法解方程组;
(4)先把方程整理为$\left\{\begin{array}{l}{3x-y=8①}\\{3x-5y=-20②}\end{array}\right.$,然后利用加减消元法解方程组.
解答 解:(1)x2=9,
x=±3,
所以x1=3,x2=-3;
(2)2(2-x)=±3,
所以x1=$\frac{1}{2}$,x2=$\frac{7}{2}$;
(3)$\left\{\begin{array}{l}{x-y=7①}\\{3x+2y=16②}\end{array}\right.$,
①×2+②得5x=30,
解得x=6,
把x=6代入①得6-y=7,
解得x=-1,
所以方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=-1}\end{array}\right.$;
(4)方程组整理为$\left\{\begin{array}{l}{3x-y=8①}\\{3x-5y=-20②}\end{array}\right.$,
①-②得4y=28,
解得y=7,
把y=7代入①得3x-7=8,解得x=5,
所以方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=7}\end{array}\right.$.
点评 本题考查了解二元一次方程组:利用加减消元法或代入消元法解方程组.

练习册系列答案
相关题目
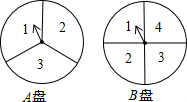 下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并分别标记了数字1,2,3和1,2,3,4.小明和小亮利用这两个转盘做游戏.规则如下:同时转动两个转盘,指针停止后,将指针所指区域的数字相加(若指针停在分界线上,则重新转动转盘),如果和为奇数,则小明获胜,如果和是偶数,则小亮获胜,请你确定游戏规则是否公平,并说明理由.
下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并分别标记了数字1,2,3和1,2,3,4.小明和小亮利用这两个转盘做游戏.规则如下:同时转动两个转盘,指针停止后,将指针所指区域的数字相加(若指针停在分界线上,则重新转动转盘),如果和为奇数,则小明获胜,如果和是偶数,则小亮获胜,请你确定游戏规则是否公平,并说明理由.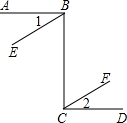 如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截,在下面三个式子只,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并写出对应的推理过程
如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截,在下面三个式子只,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并写出对应的推理过程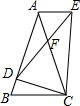 请完成下列的相似测试.
请完成下列的相似测试.