题目内容
20. 已知如图,△ABC中,AB=4,AC=2$\sqrt{2}$,∠B=30°,0°<∠C<90°.
已知如图,△ABC中,AB=4,AC=2$\sqrt{2}$,∠B=30°,0°<∠C<90°.(1)求点A到直线BC的距离以及BC的长度.
(2)将△ABC绕线段BC所在直线旋转一周,求所得几何体的表面积.
分析 (1)作AD⊥BC于D,如图,在Rt△ABD中利用含30度的直角三角形三边的关系易得AD=2,BD=2$\sqrt{3}$,然后在Rt△ACD中利用勾股定理计算出CD=2,从而得到BC的长;
(2)将△ABC绕线段BC所在直线旋转一周,所得几何体为共底面的两个圆锥,其中底面圆的半径为DA,母线长分别为BA和CA,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长计算两个圆锥的侧面积即可.
解答 解:(1)作AD⊥BC于D,如图,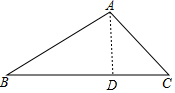
在Rt△ABD中,∵∠B=30°,
∴AD=$\frac{1}{2}$AB=2,BD=$\sqrt{3}$AD=2$\sqrt{3}$,
在Rt△ACD中,CD=$\sqrt{(2\sqrt{2})^{2}-{2}^{2}}$=2,
∴BC=BD+CD=2$\sqrt{3}$+2;
(2)将△ABC绕线段BC所在直线旋转一周,所得几何体的表面积=$\frac{1}{2}$•2π•2•4+$\frac{1}{2}$•2π•2•2$\sqrt{2}$=8π+4$\sqrt{2}$π.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了解直角三角形.

练习册系列答案
相关题目
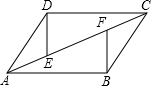 如图所示,AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,求证:BF=DE.
如图所示,AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,求证:BF=DE.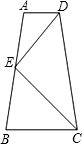 如图,已知梯形ABCD中,AD∥BC,E为AB中点,DE⊥EC.
如图,已知梯形ABCD中,AD∥BC,E为AB中点,DE⊥EC.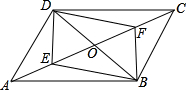 如图,在平行四边形ABCD中,已知对角线AC、BD相交于点O,若E、F是AC上两动点,分别从A、C两点以相同的速度1cm/s向点O运动.
如图,在平行四边形ABCD中,已知对角线AC、BD相交于点O,若E、F是AC上两动点,分别从A、C两点以相同的速度1cm/s向点O运动.