题目内容
 如图,已知等腰△ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求:(1)∠BDC的度数;
如图,已知等腰△ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求:(1)∠BDC的度数;(2)△ABC的周长.
考点:勾股定理的逆定理,等腰三角形的性质,勾股定理
专题:
分析:(1)首先根据BD、CD、BC长可利用勾股定理逆定理证明∠BDC=90°;
(2)设AD=xcm,则AB=AC=(x+12)cm,再利用勾股定理可得x2+162=(x+12)2,解方程可得x的值,进而得到AB长,然后可算出周长.
(2)设AD=xcm,则AB=AC=(x+12)cm,再利用勾股定理可得x2+162=(x+12)2,解方程可得x的值,进而得到AB长,然后可算出周长.
解答:解:(1)∵122+162=202,
∴DB2+CD2=BC2,
∴∠BDC=90°;
(2)设AD=xcm,则AB=AC=(x+12)cm,
∵∠BDC=90°,
∴∠ADC=90°,
∴x2+162=(x+12)2,
解得:x=
.
∴AB=AC=16
cm,
△ABC的周长是:16
+16
+20=20+33
(cm).
∴DB2+CD2=BC2,
∴∠BDC=90°;
(2)设AD=xcm,则AB=AC=(x+12)cm,
∵∠BDC=90°,
∴∠ADC=90°,
∴x2+162=(x+12)2,
解得:x=
| 14 |
| 3 |
∴AB=AC=16
| 2 |
| 3 |
△ABC的周长是:16
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
点评:此题主要考查了勾股定理,以及勾股定理逆定理,关键是掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 把一副常用三角板如图拼在一起,延长ED交AC于F.那么图中∠AFE的度数为是 ( )度.
把一副常用三角板如图拼在一起,延长ED交AC于F.那么图中∠AFE的度数为是 ( )度.| A、75 | B、105 | C、85 | D、95 |
 如图,一次函数y=kx+b的图象经过第一、三、四象限,且与反比例函数y=
如图,一次函数y=kx+b的图象经过第一、三、四象限,且与反比例函数y= 休博园内有两展览馆中国国家馆A和外国国家馆B,展馆外围有两条小道L1和L2(如图所示),现由于展馆人多天气炎热,故决定再建一个休息区C,要求休息区到两个展馆A和B的距离相等且到两条小路的距离也相等,请用直尺和圆规作图找出休息区C的位置.
休博园内有两展览馆中国国家馆A和外国国家馆B,展馆外围有两条小道L1和L2(如图所示),现由于展馆人多天气炎热,故决定再建一个休息区C,要求休息区到两个展馆A和B的距离相等且到两条小路的距离也相等,请用直尺和圆规作图找出休息区C的位置.
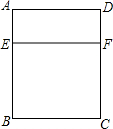 用7m长的铝合金做成透光面积(矩形ABCD的面积)为2m2的“日”型窗框(BC不超过1.3m),求窗框的宽度?(铝合金的宽度忽略不计)
用7m长的铝合金做成透光面积(矩形ABCD的面积)为2m2的“日”型窗框(BC不超过1.3m),求窗框的宽度?(铝合金的宽度忽略不计) 如图,AB∥CD,AB=CD,AE=CF,可以得到DE和BF的关系是
如图,AB∥CD,AB=CD,AE=CF,可以得到DE和BF的关系是