Question

17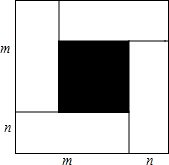．如图，大正方形由四个相同的长方形和一个小正方形组成，设长方形的两边长为m，n（m＞n），大小正方形的边长分别为x，y．观察图案，指出以下关系式：①x²-y²=4mn；②m²-n²=xy；③2n²=（x-y）²；④m²+n²=$\frac{{x}^{2}+{y}^{2}}{2}$，其中正确的是①②④（写出正确结论的序号）

Answer 1

分析 根据长方形的长和宽，结合图形进行判断，即可求解．

解答 解：由图形可知：大正方的面积-小正方形的面积=4×长方形的面积，即x²-y²=4mn，故①正确，
∵大正方形的边长x=m+n，小正方形的面积y=m-n，
∴（m+n）（m-n）=xy，即m²-n²=xy，故②正确，
∵x-y=2n，
∴4n²=（x-y）²；故③错误；
∵（m+n）²=x²，（m-n）²=y²，
∴两式相加可得m²+n²=$\frac{{x}^{2}+{y}^{2}}{2}$，故④正确．
∴正确的为①②④．
故答案为：①②④．

点评 本题考查了完全平方公式的几何背景及因式分解的应用，主要考查学生的计算能力和观察图形的能力．