题目内容
【题目】∠MON=90°,点A,B分别在OM、ON上运动(不与点O重合).
(1)如图①,AE、BE分别是∠BAO和∠ABO的平分线,随着点A、点B的运动,∠AEB= °
(2)如图②,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D
①若∠BAO=60°,则∠D= °.
②随着点A,B的运动,∠D的大小会变吗?如果不会,求∠D的度数;如果会,请说明理由.
(3)如图③,延长MO至Q,延长BA至G,已知∠BAO,∠OAG的平分线与∠BOQ的平分线及其延长线相交于点E、F,在△![]() 中,如果有一个角是另一个角的3倍,求∠ABO的度数.
中,如果有一个角是另一个角的3倍,求∠ABO的度数.



【答案】(1)135°;(2)①45°,②不发生变化,45°;(3)60°或45°
【解析】
(1)利用三角形内角和定理、两角互余、角平分线性质即可求解;
(2)①利用对顶角相等、两角互余、两角互补、角平分线性质即可求解;
②证明和推理过程同①的求解过程;
(3)由(2)的证明求解思路,不难得出![]() =90°,如果有一个角是另一个角的3倍,所以不确定是哪个角是哪个角的三倍,所以需要分情况讨论;值得注意的是,∠MON=90°,所以求解出的∠ABO一定要小于90°,注意解得取舍.
=90°,如果有一个角是另一个角的3倍,所以不确定是哪个角是哪个角的三倍,所以需要分情况讨论;值得注意的是,∠MON=90°,所以求解出的∠ABO一定要小于90°,注意解得取舍.
(1)
(2)①如图所示

AD与BO交于点E,

②∠D的度数不随A、B的移动而发生变化
设![]() ,因为AD平分∠BAO,所以
,因为AD平分∠BAO,所以![]() ,因为∠AOB=90°,所以
,因为∠AOB=90°,所以![]() 。因为BC平分
。因为BC平分![]() ,所以
,所以![]() 。又因为
。又因为![]() 。所以
。所以![]()
(3)因为∠BAO与∠BOQ的平分线交于点E,
所以![]() ,
,
所以![]()
因为AE、AF分别是∠BAO和∠OAG的平分线,
所以![]() 在△AEF中,若有一个角是另一个角的3倍,
在△AEF中,若有一个角是另一个角的3倍,
则①当![]() 时,得
时,得![]() ,此时
,此时![]()
②当![]() 时,得
时,得![]() ,此时
,此时![]() ,舍去。
,舍去。
③当![]() 时,得
时,得![]() ,此时
,此时![]()
④当![]() 时,得
时,得![]() ,此时
,此时![]() ,舍去。
,舍去。
综上可知,∠ABO的度数为60°或45°。

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).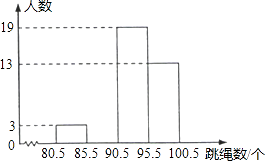
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是个,中位数是个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.