题目内容
【题目】在一条直线上依次有A,B,C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(时)后,与B港的距离为y(海里),y与x之间的函数图象如图所示.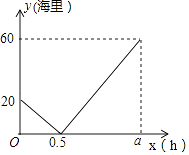
(1)A,C两港口间的距离为海里,a=
(2)求y与x之间的函数关系式.
(3)在B岛上有一个不间断发射信号的信号发射台,发射的信号覆盖半径为8海里的圆形区域,求该海巡船鞥接受到该信号的时间有多长?
【答案】
(1)80,2h
(2)解:当0<x≤0.5时,设y与x的函数关系式为:y=kx+b,
∵函数图象经过点(0,20),(0.5,0)
∴ ![]() ,
,
解得 ![]() .
.
所以,y=﹣0x+20;
当0.5<x≤1.7时,设y与x的函数关系式为:y=mx+n,
∵函数图象经过点(0.5,0),(2,60),
∴ ![]() ,
,
解得 ![]() .
.
所以,y=40x﹣20,
(3)解:当0≤x≤0.5,y=8时,﹣40x+20=8,
解得x=0.3,
当0.5<x≤2,y=8时,40x﹣20=8,
解得x=0.7,
∴0.7﹣0.3=0.4
答:该海巡船能接受到该信号的时间为:0.4h.
【解析】解:(1)由图可知,A、B港口间的距离为20,B、C港口间的距离为60,
所以,A、C港口间的距离为:20+60=80km,
海巡船的速度为:20÷0.5=40km/h,
∴a=80÷40=2h,
所以答案是:80,2h;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目