Question

【题目】如图所示，等边三角形ABC放置在平面直角坐标系中，已知A（0，0）、B（6，0），反比例函数的图象经过点C．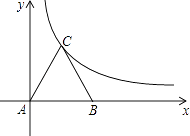

（1）求点C的坐标及反比例函数的解析式．
（2）将等边△ABC向上平移n个单位，使点B恰好落在双曲线上，求n的值．

Answer 1

【答案】
（1）解：过C点作CD⊥x轴，垂足为D

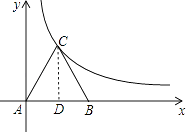
，设反比例函数的解析式为y= ，

∵△ABC是等边三角形，

∴AC=AB=6，∠CAB=60°，

∴AD=3，CD=sin60°×AC= ×6=3 ，

∴点C坐标为（3，3 ），

∵反比例函数的图象经过点C，

∴k=9 ，

∴反比例函数的解析式y= ；

（2）解：若等边△ABC向上平移n个单位，使点B恰好落在双曲线上，

则此时B点的横坐标为6，

即纵坐标y= = ，也是向上平移n= ．

【解析】（1）利用等边三角形的性质和三角函数的定义求出C坐标，利用待定系数法可求出反比例函数的解析式; （2）利用点向上平移时，坐标的变化规律，横同纵加，利用平移后横纵之积为,建立方程，求出n.
【考点精析】解答此题的关键在于理解反比例函数的概念的相关知识，掌握形如y＝k/x（k为常数，k≠0）的函数称为反比例函数．自变量x的取值范围是x不等于0的一切实数，函数的取值范围也是一切非零实数．