Question

【题目】如图，已知：Rt△ABC中，∠C＝90°，AC＝BC＝2，将一块三角尺的直角顶点与斜边AB的中点M重合，当三角尺绕着点M旋转时，两直角边始终保持分别与边BC、AC交于D，E两点（D、E不与B、A重合）．

（1）求证：MD＝ME；

（2）求四边形MDCE的面积；

Answer 1

【答案】（1）证明见解析（2）1

【解析】

（1）连接CM，根据∠BMD＝90°﹣∠DMC，∠EMC＝90°﹣∠DMC，可证明∠BMD=∠CME，根据等腰直角三角形的性质可得∠B＝∠MCA=45°．根据直角三角形斜边中线的性质可得CM=BM，即可证明△BDM≌△CEM，然后即可证MD=ME；（2）利用三角形全等可知四边形MDCE的面积等于△CMB的面积，即可得答案.

（1）证明：连接CM，在Rt△ABC中，M是AB的中点，且AC＝BC，

∴CM＝AB＝BM，

∠MCA＝∠B＝45°，CM⊥AB，

而∠BMD＝90°﹣∠DMC，∠EMC＝90°﹣∠DMC．

∴∠BMD＝∠EMC．

△BDM≌△CEM（ASA）．

∴MD＝ME

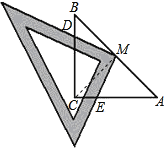
（2）∵△BDM≌△CEM，

∴S四边形MDCE＝S△DMC+S△CME＝S△DMC+S△BMD＝S△BCM＝S△ACB＝××2×2=1.

∴四边形MDCE的面积为1；