题目内容
10.在半径为1的圆O中,弦AB=$\sqrt{2}$,弦AC=$\sqrt{3}$,求∠BAC的大小.分析 先根据题意画出图形,分别作AC、AB的垂线,连接OA,再根据锐角三角函数的定义求出∠AOD及∠AOE的度数,根据直角三角形的性质即可得出结论.
解答 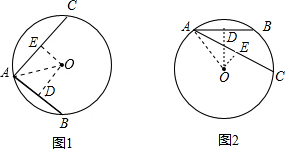 解:①如图1,两弦在圆心的异侧时,过O作OD⊥AB于点D,OE⊥AC于点E,连接OA,
解:①如图1,两弦在圆心的异侧时,过O作OD⊥AB于点D,OE⊥AC于点E,连接OA,
∵AB=$\sqrt{2}$,AC=$\sqrt{3}$,
∴AD=$\frac{\sqrt{2}}{2}$,AE=$\frac{\sqrt{3}}{2}$,
根据直角三角形中三角函数的值可知:sin∠AOD=$\frac{\sqrt{2}}{2}$,
∴∠AOD=45°,
∵sin∠AOE=$\frac{\sqrt{3}}{2}$,
∴∠AOE=60°,
∴∠OAD=90°-∠AOD=45°,∠OAC=90°-∠AOE=30°
∴∠BAC=∠OAD+∠OAC=45°+30°=75°;
②如图2,当两弦在圆心的同侧时同①可知∠AOD=45°,∠AOE=60°,
∴∠AOE=60°,
∴∠OAC=90°-∠AOE=90°-60°=30°,∠OAB=90°-∠AOD=90°-45°=45°.
∴∠BAC=∠OAB-∠OAC=45°-30°=15°,
即∠BAC=75°或15°.
点评 本题考查的是垂径定理及勾股定理,解直角三角形,锐角三角函数的定义及特殊角的三角函数,解答此题时要注意分类讨论,不要漏解.

练习册系列答案
相关题目
2.下列命题中属于真命题的是( )
| A. | 多边形的内角和等于180° | B. | 全等三角形的对应边相等 | ||
| C. | 两个锐角相等 | D. | 若a>b,则a2>b2 |
19.“十、一”黄金周期间,阜阳生态园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
(1)若9月30日的游客人数记为a,请用a的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)若9月30日的游客人数为5千人,门票每人10元.问黄金周期间阜阳生态园门票收入是多少元?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 单位:千人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)若9月30日的游客人数为5千人,门票每人10元.问黄金周期间阜阳生态园门票收入是多少元?




 如图,在不规则五角星ABCDE中,∠ADB的角平分线与∠AMB的角平分线相交于点P,请∠P,∠A,∠B之间的等量关系,说明你的理由.
如图,在不规则五角星ABCDE中,∠ADB的角平分线与∠AMB的角平分线相交于点P,请∠P,∠A,∠B之间的等量关系,说明你的理由.