题目内容
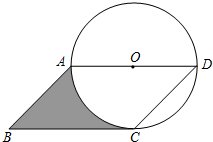 如图,已知?ABCD,∠B=45°,以AD为直径的⊙O经过点C.
如图,已知?ABCD,∠B=45°,以AD为直径的⊙O经过点C.(1)求证:直线BC是⊙O的切线;
(2)若AB=2
| 2 |
考点:切线的判定,扇形面积的计算
专题:
分析:(1)连结OC,根据平行四边形的性质求得∠D=45°,然后根据等边对等角,得出∠OCD=45°,从而求得∠COD=90°,再根据平行线的性质得出OC⊥BC,即可求得BC是⊙O的切线.
(2)根据S阴影部分=S□ABCD-SRt△COD-S扇形AOC即可求得;
(2)根据S阴影部分=S□ABCD-SRt△COD-S扇形AOC即可求得;
解答:(1)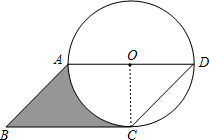 证明:连结OC.
证明:连结OC.
∵四边形ABCD是平行四边形,
∴∠D=∠B=45°.
∵OC=OD,
∴∠OCD=∠D=45°,
∴∠DOC=90°.
∵AD∥BC,
∴∠OCB=∠DOC=90°,
∴直线BC是⊙O的切线.
(2)解:在Rt△DOC中,CD=AB=2
,∠D=45°,
∴OC=CDsin∠D=2
sin45°=2,
∴AD=2OC=4.
S阴影部分=S□ABCD-SRt△COD-S扇形AOC
=4×2-
×2×2-
π×22
=6-π.
答:阴影部分的面积为(6-π).
 证明:连结OC.
证明:连结OC.∵四边形ABCD是平行四边形,
∴∠D=∠B=45°.
∵OC=OD,
∴∠OCD=∠D=45°,
∴∠DOC=90°.
∵AD∥BC,
∴∠OCB=∠DOC=90°,
∴直线BC是⊙O的切线.
(2)解:在Rt△DOC中,CD=AB=2
| 2 |
∴OC=CDsin∠D=2
| 2 |
∴AD=2OC=4.
S阴影部分=S□ABCD-SRt△COD-S扇形AOC
=4×2-
| 1 |
| 2 |
| 1 |
| 4 |
=6-π.
答:阴影部分的面积为(6-π).
点评:此题考查学生会利用转化的思想把不规则图形的面积转化为规则图形的面积,考查了数形结合的数学思想,同时要求学生掌握平行四边形及等腰直角三角形的性质,是一道中档题.

练习册系列答案
相关题目
已知⊙O的半径r=5,圆心O到直线l的距离为d=3,则直线l与⊙O的位置关系是( )
| A、相交 | B、相切 |
| C、相离 | D、以上都不对 |
 如图,已知∠A=∠C,∠E=∠F,那么AB∥CD吗?为什么?
如图,已知∠A=∠C,∠E=∠F,那么AB∥CD吗?为什么?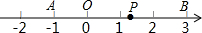 如图,点O是数轴的原点,且数轴上的点A和点B对应的数分别为-1和3,数轴上一动点P对应的数为x.
如图,点O是数轴的原点,且数轴上的点A和点B对应的数分别为-1和3,数轴上一动点P对应的数为x. 学校有一块长为30米,宽为20米的长方形空地,准各在这块空地上修筑两条互相垂直的通道,将这快空地分成四个小长方形,在这些小长方形空地上种植花草.设道路的宽都是x米.
学校有一块长为30米,宽为20米的长方形空地,准各在这块空地上修筑两条互相垂直的通道,将这快空地分成四个小长方形,在这些小长方形空地上种植花草.设道路的宽都是x米.