题目内容
我们知道sin30°=
,tan30°=
,sin45°=
,tan45°=1,sin60°=
,tan60°=
,由此可以得到什么规律,对于任意锐角α,规律成立吗?你能否用锐角三角函数的定义加以证明?
| 1 |
| 2 |
| ||
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
考点:锐角三角函数的定义,特殊角的三角函数值
专题:规律型
分析:根据已知条件可以得出sin230°+sin260°=sin245°+sin245°=1,tan30°•tan60°=tan45°•tan45°=1,由此得到规律:对于任意锐角α,sin2α+sin2(90°-α)=1,tanα•tan(90°-α)=1,利用锐角三角函数的定义证明即可.
解答: 解:∵sin30°=
解:∵sin30°=
,tan30°=
,sin45°=
,tan45°=1,sin60°=
,tan60°=
,
∴sin230°+sin260°=sin245°+sin245°=1,tan30°•tan60°=tan45°•tan45°=1,
由此得到规律:对于任意锐角α,sin2α+sin2(90°-α)=1,tanα•tan(90°-α)=1.理由如下:
如图,△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,设∠A=α,则∠B=90°-α.
由勾股定理,得a2+b2=c2,
∵sinA=
,sinB=
,tanA=
,tanB=
,
∴sin2α+sin2(90°-α)=sin2A+sin2B=(
)2+(
)2=
=
=1,
tanα•tan(90°-α)=tanA•tanB=
×
=1.
 解:∵sin30°=
解:∵sin30°=| 1 |
| 2 |
| ||
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
∴sin230°+sin260°=sin245°+sin245°=1,tan30°•tan60°=tan45°•tan45°=1,
由此得到规律:对于任意锐角α,sin2α+sin2(90°-α)=1,tanα•tan(90°-α)=1.理由如下:
如图,△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,设∠A=α,则∠B=90°-α.
由勾股定理,得a2+b2=c2,
∵sinA=
| a |
| c |
| b |
| c |
| a |
| b |
| b |
| a |
∴sin2α+sin2(90°-α)=sin2A+sin2B=(
| a |
| c |
| b |
| c |
| a2+b2 |
| c2 |
| c2 |
| c2 |
tanα•tan(90°-α)=tanA•tanB=
| a |
| b |
| b |
| a |
点评:本题考查了锐角三角函数的定义,在Rt△ABC中,∠C=90°.
(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
即sinA=∠A的对边:斜边=a:c.
(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
即cosA=∠A的邻边:斜边=b:c.
(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
即tanA=∠A的对边:∠A的邻边=a:b.
(4)三角函数:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
即sinA=∠A的对边:斜边=a:c.
(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
即cosA=∠A的邻边:斜边=b:c.
(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
即tanA=∠A的对边:∠A的邻边=a:b.
(4)三角函数:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )| A、40° | B、45° |
| C、50° | D、55° |
 如图,有点A、B、C、D,请画出一点P,使PA=PB,PC=PD.
如图,有点A、B、C、D,请画出一点P,使PA=PB,PC=PD. 如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点,与x轴的正半轴交于C点,抛物线的顶点为D,连接BC、BD,抛物线上是否存在一点P,使得∠PCB=∠CBD?若存在,求出P点坐标.
如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点,与x轴的正半轴交于C点,抛物线的顶点为D,连接BC、BD,抛物线上是否存在一点P,使得∠PCB=∠CBD?若存在,求出P点坐标.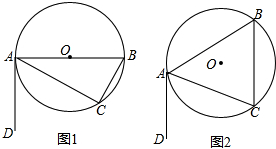 如图1,⊙O中,AB为直径,AC为弦,过A作直线DA,使∠DAC=∠B.
如图1,⊙O中,AB为直径,AC为弦,过A作直线DA,使∠DAC=∠B. 如图,△ABC中,∠B=90°,AB=6,BC=8,点P从点A开始沿边AB向点B以km/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动,问:
如图,△ABC中,∠B=90°,AB=6,BC=8,点P从点A开始沿边AB向点B以km/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动,问: 如图,A,B,C三个居民小区在位置上成三角形,现决定在三个小区之间修建一个购物超市,若超市到三个小区的距离相等,则超市应建在
如图,A,B,C三个居民小区在位置上成三角形,现决定在三个小区之间修建一个购物超市,若超市到三个小区的距离相等,则超市应建在