题目内容
已知AB是⊙O的直径,弦CD交AB于点E,AB=6,
=
.
(1)当∠AEC=90°时,求CD的长;
(2)当∠AEC=30°时,求CD的长.
| BE |
| OE |
| 1 |
| 2 |
(1)当∠AEC=90°时,求CD的长;
(2)当∠AEC=30°时,求CD的长.
考点:垂径定理
专题:
分析:(1)连接OC.根据AB=6,
=
,求得OE的长,根据勾股定理求得CE的长,再根据垂径定理即可求得CD的长.
(2)利用垂径定理和勾股定理和相交弦求解.
| BE |
| OE |
| 1 |
| 2 |
(2)利用垂径定理和勾股定理和相交弦求解.
解答: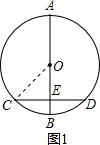 解:(1)如图1,连接OC.
解:(1)如图1,连接OC.
∵AB=6,
∴OC=OB=3,
∵
=
.
∴OE=2,
在直角三角形OEC中,根据勾股定理,得
CE=
.
∵AB⊥CD于E,
∴CD=2CE=2
.
(2)如图2,过O作OP⊥CD于E,
∵AB=6,
=
,
∴BE=1,OE=2,AE=5,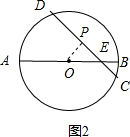
∵∠AEC=30°,
∴在Rt△POE中,OE=2,
∴PE=OPcos30°=2×
=
设CE=x,利用相交弦定理可得:1×5=(x-
)(x+
)
解得x=2
,
所以CD=4
.
 解:(1)如图1,连接OC.
解:(1)如图1,连接OC.∵AB=6,
∴OC=OB=3,
∵
| BE |
| OE |
| 1 |
| 2 |
∴OE=2,
在直角三角形OEC中,根据勾股定理,得
CE=
| 5 |
∵AB⊥CD于E,
∴CD=2CE=2
| 5 |
(2)如图2,过O作OP⊥CD于E,
∵AB=6,
| BE |
| OE |
| 1 |
| 2 |
∴BE=1,OE=2,AE=5,

∵∠AEC=30°,
∴在Rt△POE中,OE=2,
∴PE=OPcos30°=2×
| ||
| 2 |
| 3 |
设CE=x,利用相交弦定理可得:1×5=(x-
| 3 |
| 3 |
解得x=2
| 2 |
所以CD=4
| 2 |
点评:本题的关键是利用垂径定理和勾股定理和相交弦定理求线段的长.

练习册系列答案
相关题目
 如图,BC为⊙O的直径,BC=4
如图,BC为⊙O的直径,BC=4
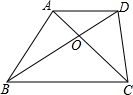 如图所示,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD:BC=2:3,求S△AOD:S△BOA.
如图所示,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD:BC=2:3,求S△AOD:S△BOA.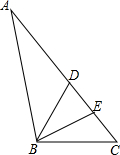 已知在△ABC中,D是边AC上的一点,∠CBD的角平分线交AC于点E,且AE=AB,求证:AE2=AD•AC.
已知在△ABC中,D是边AC上的一点,∠CBD的角平分线交AC于点E,且AE=AB,求证:AE2=AD•AC. 如图,有点A、B、C、D,请画出一点P,使PA=PB,PC=PD.
如图,有点A、B、C、D,请画出一点P,使PA=PB,PC=PD. 如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点,与x轴的正半轴交于C点,抛物线的顶点为D,连接BC、BD,抛物线上是否存在一点P,使得∠PCB=∠CBD?若存在,求出P点坐标.
如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点,与x轴的正半轴交于C点,抛物线的顶点为D,连接BC、BD,抛物线上是否存在一点P,使得∠PCB=∠CBD?若存在,求出P点坐标. 如图,A,B,C三个居民小区在位置上成三角形,现决定在三个小区之间修建一个购物超市,若超市到三个小区的距离相等,则超市应建在
如图,A,B,C三个居民小区在位置上成三角形,现决定在三个小区之间修建一个购物超市,若超市到三个小区的距离相等,则超市应建在