题目内容
求证:|a|-|b|≤|a-b|.
考点:绝对值
专题:
分析:分四种情况:①a<0,b<0;②a<0,b≥0;③a≥0,b<0;④a≥0,b≥0;进行讨论即可求解.
解答:证明:①当a<0,b<0时,
|a|-|b|=-a+b,
|a-b|=a-b或-a+b,
∵-a+b<a-b,-a+b=-a+b,
∴|a|-|b|≤|a-b|;
②当a<0,b≥0时,
|a|-|b|=-a-b,
|a-b|=-a+b,
∵-a-b≤-a+b,
∴|a|-|b|≤|a-b|;
③当a≥0,b<0时,
|a|-|b|=a+b,
|a-b|=a-b,
∵a+b<a-b,
∴|a|-|b|<|a-b|;
④当a≥0,b≥0时,
|a|-|b|=a-b,
|a-b|=a-b或-a+b,
∵a-b=a-b,a-b≤-a+b,
∴|a|-|b|≤|a-b|.
综上所述,|a|-|b|≤|a-b|.
|a|-|b|=-a+b,
|a-b|=a-b或-a+b,
∵-a+b<a-b,-a+b=-a+b,
∴|a|-|b|≤|a-b|;
②当a<0,b≥0时,
|a|-|b|=-a-b,
|a-b|=-a+b,
∵-a-b≤-a+b,
∴|a|-|b|≤|a-b|;
③当a≥0,b<0时,
|a|-|b|=a+b,
|a-b|=a-b,
∵a+b<a-b,
∴|a|-|b|<|a-b|;
④当a≥0,b≥0时,
|a|-|b|=a-b,
|a-b|=a-b或-a+b,
∵a-b=a-b,a-b≤-a+b,
∴|a|-|b|≤|a-b|.
综上所述,|a|-|b|≤|a-b|.
点评:考查了绝对值,分类思想的应用,关键是分四种情况讨论求解.

练习册系列答案
相关题目
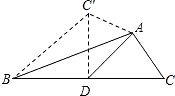 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在点C′的位置,则图中的一个等腰直角三角形是( )
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在点C′的位置,则图中的一个等腰直角三角形是( )| A、△ADC | B、△BDC′ |
| C、△ADC′ | D、不存在 |
 分别在下图中画出△ABC绕点O顺时针旋转90°和180°后的图形.
分别在下图中画出△ABC绕点O顺时针旋转90°和180°后的图形.