题目内容
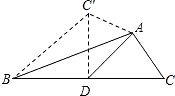 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在点C′的位置,则图中的一个等腰直角三角形是( )
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在点C′的位置,则图中的一个等腰直角三角形是( )| A、△ADC | B、△BDC′ |
| C、△ADC′ | D、不存在 |
考点:翻折变换(折叠问题)
专题:
分析:由三角形中线的定义,可得BD=CD,又由折叠的性质,易求得∠BDC′=90°,BD=C′D,即可得△BDC′是等腰直角三角形.
解答:解:∵AD是△ABC的中线,
∴BD=CD,
由折叠的性质可得:C′D=CD,∠ADC′=∠ADC=45°,
∴∠CDC′=90°,C′D=BD,
∴∠BDC′=180°-∠CDC′=90°,
∴△BDC′是等腰直角三角形.
故选:B.
∴BD=CD,
由折叠的性质可得:C′D=CD,∠ADC′=∠ADC=45°,
∴∠CDC′=90°,C′D=BD,
∴∠BDC′=180°-∠CDC′=90°,
∴△BDC′是等腰直角三角形.
故选:B.
点评:此题考查了折叠的性质、等腰直角三角形的判定以及三角形中线的定义.此题难度不大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
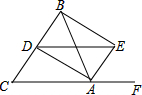 如图,△ABC中,AB=AC,F是CA延长线上一点,AD、AE分别平分∠BAC和∠BAF,BE⊥AE,说明:AB=DE.
如图,△ABC中,AB=AC,F是CA延长线上一点,AD、AE分别平分∠BAC和∠BAF,BE⊥AE,说明:AB=DE.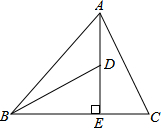 已知在△ABC中,AE⊥BC于E,AE=BE,D是AE上一点,且DE=CE,连接BD,AC,试判断BD与AC的位置关系与数量关系,并说明理由.
已知在△ABC中,AE⊥BC于E,AE=BE,D是AE上一点,且DE=CE,连接BD,AC,试判断BD与AC的位置关系与数量关系,并说明理由.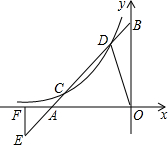 已知直线y=x+3与x轴、y轴分别交于A,B点,与y=
已知直线y=x+3与x轴、y轴分别交于A,B点,与y=