Question

18．完成下列各题
（1）如图1△ABC中∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于E．求证：△ACD≌△AED．
（2）如图2，∠1与∠D互余，CF⊥DF．求证：AB∥CD．

Answer 1

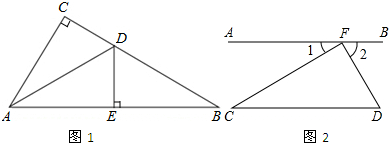
分析 （1）根据角平分线的性质得出DC=DE，由HL定理得出△ACD≌△AED；
（2）根据平角的定义得出∠1+∠CFD+∠2=180°，再由∠1与∠D互余，CF⊥DF得∠1=∠C，从而得出AB∥CD．

解答 证明：（1）∵AD平分∠CAB，∠C=90°，DE⊥AB，
∴DC=DE，
在Rt△ACD和Rt△AED中，
$\left\{\begin{array}{l}{AD=AD}\\{DC=DE}\end{array}\right.$，
∴Rt△ACD≌Rt△AED，
（2）∵CF⊥DF，
∴∠C+∠D=90°，
∵∠1与∠D互余，
∴∠1=∠C，
∴AB∥CD．

点评 本题考查了全等三角形的判定以及平行线的判定，掌握全等三角形的判定方法以及平行线的判定方法是解题的关键．