题目内容
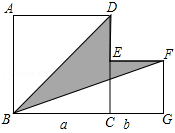
20. 如图,AC⊥CB,AD为△ABC的中线,CG为高,DE⊥AD,BC=2AC,求证:AD=DF+DE.
如图,AC⊥CB,AD为△ABC的中线,CG为高,DE⊥AD,BC=2AC,求证:AD=DF+DE.
分析 根据余角的性质得到∠CAD=∠BDE,∠ACF=∠B,由已知条件得到BD=AC=$\frac{1}{2}$BC,推出△ACF≌△BDE,根据全等三角形的性质得到AF=DE,于是得到结论.
解答 解:∵AC⊥CB,DE⊥AD,
∴∠CAD+∠ADC=∠ADC+∠BDE=90°,
∴∠CAD=∠BDE,
∵CG⊥AB,
∴∠ACF+∠BCF=∠B+∠BCG=90°,
∴∠ACF=∠B,
∵AD为△ABC的中线,BC=2AC,
∴BD=AC=$\frac{1}{2}$BC,
在△ACF与△BDE中,$\left\{\begin{array}{l}{∠ACF=∠B}\\{AC=BD}\\{∠CAF=∠BDE}\end{array}\right.$,
∴△ACF≌△BDE,
∴AF=DE,
∵AD=AF+DF,
∴AD=DF+DE.
点评 本题考查了全等三角形的判定和性质,直角三角形的性质,余角的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
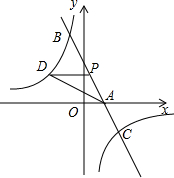 如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5),C($\frac{5}{2}$,d)两点,点M是y轴上一动点,点P(m,n)是一次函数y=kx+b的图象上的动点.
如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5),C($\frac{5}{2}$,d)两点,点M是y轴上一动点,点P(m,n)是一次函数y=kx+b的图象上的动点. 如图,在△ABC中,AB=10,∠B=60°,BC=16,P、Q分别在边BC、AB上,且BP=BQ,连接PQ并延长与CA的延长线交于点R.
如图,在△ABC中,AB=10,∠B=60°,BC=16,P、Q分别在边BC、AB上,且BP=BQ,连接PQ并延长与CA的延长线交于点R.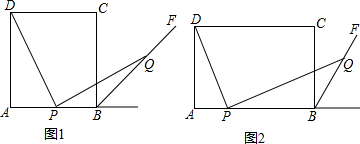
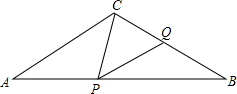 如图,在△ABC中,AC=BC=10,AB=16,点P在边AB上(不与点A,B重合),作∠CPQ=∠A,PQ交BC于Q,设AP=x,BQ=y.
如图,在△ABC中,AC=BC=10,AB=16,点P在边AB上(不与点A,B重合),作∠CPQ=∠A,PQ交BC于Q,设AP=x,BQ=y.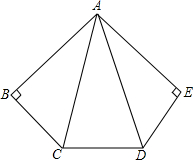 如图,AB⊥BC,AE⊥ED,AB=AE,∠ACD=∠ADC,求证:BC=ED.
如图,AB⊥BC,AE⊥ED,AB=AE,∠ACD=∠ADC,求证:BC=ED. 如图,正方形ABCD,点E是对角线AC上一点,连接BE,过E作EF⊥BE,EF交CD于F,若AE=2$\sqrt{2}$,CF=5,则正方形ABCD的面积为81.
如图,正方形ABCD,点E是对角线AC上一点,连接BE,过E作EF⊥BE,EF交CD于F,若AE=2$\sqrt{2}$,CF=5,则正方形ABCD的面积为81.