Question

3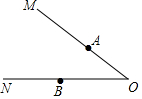．如图，已知∠MON，点A，B分别在OM，ON边上，且OA=OB．
（1）求作：过点A，B分别作OM，ON的垂线，两条垂线的交点记作点D（保留作图痕迹，不写作法）；
（2）连接OD，若∠MON=50°，则∠ODB=65°．

Answer 1

分析 （1）根据过直线上一点作直线垂线的方法作出垂线即可；
（2）利用全等三角形的判定与性质结合四边形内角和定理得出答案．

解答 解：（1）如图，DA，DB即为所求垂线；

（2）连接OD，
∵DB⊥ON，DA⊥OM，
∴∠OBD=∠OAD=90°，∠MON=50°，
∴∠ADB=180°-50°=130°．
在Rt△OBD与Rt△OAD中，
∵$\left\{\begin{array}{l}{OB=OA}\\{OD=OD}\end{array}\right.$，
∴Rt△OBD≌Rt△OAD（HL），
∴∠ODB=$\frac{1}{2}$∠ADB=65°．
故答案为：65．

点评 此题主要考查了基本作图以及全等三角形的判定与性质，正确得出Rt△OBD≌Rt△OAD是解题关键．