题目内容
某电子厂生产一种显示器,每件成本1400元,定价2000元.一位电脑销售商欲订购120个这种显示器,并提出:“显示器单价每降价10元,就多订购4个.”按这位销售商的要求,电子厂每个显示器售价为多少时利润最大?最大利润是多少?
考点:二次函数的应用
专题:
分析:利用总利润=每一个的利润×售出的个数列出关系式,利用配方法解决问题即可.
解答:解:设每一个显示器降价x元,总利润为w,由题意得
w=(2000-1400-x)(120+
×4)
=-
x2+120x+72000
=-
(x-150)2+81000
当x=150时,w取得最大值为81000.
即售价为2000-150=1850元时,利润最大,最大为81000元.
w=(2000-1400-x)(120+
| x |
| 10 |
=-
| 2 |
| 5 |
=-
| 2 |
| 5 |
当x=150时,w取得最大值为81000.
即售价为2000-150=1850元时,利润最大,最大为81000元.
点评:此题考查二次函数的实际运用,理解题意,根据题目蕴含的数量关系列出函数解析式是解决问题的关键.

练习册系列答案
相关题目
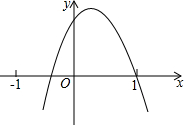 如图,抛物线y=ax2+bx+c的开口向下,交x轴的正半轴于(1,0),则下列结论错误的是( )
如图,抛物线y=ax2+bx+c的开口向下,交x轴的正半轴于(1,0),则下列结论错误的是( )| A、abc<0 |
| B、a-b+c<0 |
| C、2a+b>0 |
| D、a+c<0 |
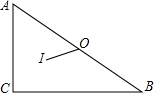 如图,△ABC中,∠C=90°,AC=3,BC=4,O为△ABC的外心,I为△ABC的内心,求OI的长.
如图,△ABC中,∠C=90°,AC=3,BC=4,O为△ABC的外心,I为△ABC的内心,求OI的长.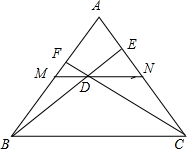 如图,在等边△ABC中,M、N分别是AB、AC的中点,D为MN上任意一点,BD、CD的延长线分别交AC、AB于点E、F,求证:
如图,在等边△ABC中,M、N分别是AB、AC的中点,D为MN上任意一点,BD、CD的延长线分别交AC、AB于点E、F,求证:
 如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是
如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是 如图,CD是△ABC的中线,AC=3cm,BC=4cm,则△ACD的周长比△BCD的周长少
如图,CD是△ABC的中线,AC=3cm,BC=4cm,则△ACD的周长比△BCD的周长少