题目内容
12.下列命题中是假命题的是( )| A. | 如果一个直角三角形的两条直角边与另一个直角三角形的两条直角边对应相等,那么这两个直角三角形全等 | |
| B. | 等腰三角形顶角的平分线把它分成两个全等的三角形 | |
| C. | 周长相等的两个三角形全等 | |
| D. | 有一条直角边对应相等的两个等腰直角三角形全等 |
分析 根据全等三角形的判定方法容易得出A、B、D是真命题,C是假命题,即可得出结论.
解答 解:A.两条直角边对应相等的两个直角三角形,根据两三角形全等的判定定理“SAS”得出两个三角形全等;故本选项是真命题;
B.已知等腰三角形的两腰相等,顶角平分线为公共边,则其根据为“SAS”可以得出两个三角形全等,故本选项是真命题;
C.周长相等的两个三角形不一定全等;故本选项是假命题;
D.有一条直角边对应相等的两个等腰直角三角形,根据两三角形全等的判定定理“SAS”得出两个三角形全等;故本选项是真命题;
故选:C.
点评 此题主要考查了命题与定理以及全等三角形的判定方法,熟练掌握全等三角形的判定定理是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 已知:如图,AB⊥CD于O,EF为经过点O的一条直线,那么∠1与∠2的关系是( )
已知:如图,AB⊥CD于O,EF为经过点O的一条直线,那么∠1与∠2的关系是( )
 已知:如图,AB⊥CD于O,EF为经过点O的一条直线,那么∠1与∠2的关系是( )
已知:如图,AB⊥CD于O,EF为经过点O的一条直线,那么∠1与∠2的关系是( )| A. | 互余 | B. | 互补 | C. | 互为对顶角 | D. | 相等 |
4. 如图,将△ABC进行平移得到△MNL,其中点A的对应点是点M,则下列结论中不一定成立的是( )
如图,将△ABC进行平移得到△MNL,其中点A的对应点是点M,则下列结论中不一定成立的是( )
 如图,将△ABC进行平移得到△MNL,其中点A的对应点是点M,则下列结论中不一定成立的是( )
如图,将△ABC进行平移得到△MNL,其中点A的对应点是点M,则下列结论中不一定成立的是( )| A. | AM∥BN | B. | AM=BN | C. | BC=ML | D. | BN∥CL |
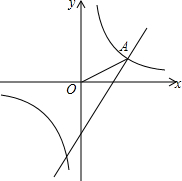 如图,在同一直角坐标系中,一次函数y=$\sqrt{3}$x-2的图象和反比例函数y=$\frac{k}{x}$的图象的一个交点为A($\sqrt{3}$,m).
如图,在同一直角坐标系中,一次函数y=$\sqrt{3}$x-2的图象和反比例函数y=$\frac{k}{x}$的图象的一个交点为A($\sqrt{3}$,m).