题目内容
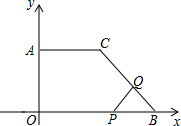 如图,直角坐标系中有直角梯形AOBC,点A在y轴正半轴上,点B在x轴正半轴上,AC∥OB,AC=6cm,AO=8cm,OB=12cm.
如图,直角坐标系中有直角梯形AOBC,点A在y轴正半轴上,点B在x轴正半轴上,AC∥OB,AC=6cm,AO=8cm,OB=12cm.(1)求BC的长;
(2)动点P、Q都从点B出发,点P沿B→O方向做匀速运动,到点O处停止;点Q沿B→C→A方向做匀速运动,到点A处停止.若点P的速度是1cm/s,点Q的速度是3cm/s:
①运动过程中是否存在某一时刻,以P、B、C、Q为顶点的四边形是平行四边形?说明理由.
②连接PQ,直线PQ是否能把梯形ACBO的周长和面积同时平分?说明理由.
(3)若P在线段OB上,Q在线段AC上,直线PQ在经过梯形内某点时,一定能将梯形分成面积相等的两部分,请直接写出该点坐标.
考点:四边形综合题
专题:
分析:(1)作CD⊥OB于D,得到矩形OACD,根据矩形的性质得出OD=AC=6cm,CD=AO=8cm,那么BD=OB-OD=6cm,然后在Rt△BCD中,利用勾股定理即可求出BC=
=10cm;
(2)①由于BP∥CQ,所以当BP=CQ时,以P、B、C、Q为顶点的四边形是平行四边形.分0<t≤
;
<t<
;
≤t≤12三种情况进行讨论;
②先分别求出梯形ACBO的周长及面积,再求出直线PQ把梯形的周长平分时的t值,将此时的t值代入求BPQC的面积,如果所求值是梯形ACBO面积的一半,说明能够;否则不能;
(3)设AC中点为E,OB中点为F,连结EF,过EF中点G的直线一定能将梯形分成面积相等的两部分.根据中点坐标公式求解即可.
| BD2+CD2 |
(2)①由于BP∥CQ,所以当BP=CQ时,以P、B、C、Q为顶点的四边形是平行四边形.分0<t≤
| 10 |
| 3 |
| 10 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
②先分别求出梯形ACBO的周长及面积,再求出直线PQ把梯形的周长平分时的t值,将此时的t值代入求BPQC的面积,如果所求值是梯形ACBO面积的一半,说明能够;否则不能;
(3)设AC中点为E,OB中点为F,连结EF,过EF中点G的直线一定能将梯形分成面积相等的两部分.根据中点坐标公式求解即可.
解答: 解:(1)如图,作CD⊥OB于D,则四边形OACD是矩形,
解:(1)如图,作CD⊥OB于D,则四边形OACD是矩形,
OD=AC=6cm,CD=AO=8cm.
在Rt△BCD中,∵∠BDC=90°,BD=OB-OD=6cm,CD=8cm,
∴BC=
=10cm;
(2)①∵BP∥CQ,
∴当BP=CQ时,以P、B、C、Q为顶点的四边形是平行四边形.
如果0<t≤
时,Q在线段BC上,显然t不存在;
如果
<t<
时,Q在线段AC上,当t=3t-10,即t=5时,以P、B、C、Q为顶点的四边形是平行四边形;
如果
≤t≤12时,Q在A点,当当BP=CA,即t=6时,以P、B、C、Q为顶点的四边形是平行四边形;
综上所述,运动过程中存在t=5s或6s,以P、B、C、Q为顶点的四边形是平行四边形;
②不存在,理由如下:
∵梯形ACBO的周长和面积分别为:
周长=6+8+12+10=36(cm),面积=
(6+12)×8=72(cm2).
若当线段PQ平分梯形ACBO的周长时,Q在AC上,则BP+BC+CQ=
×36=18,
即t+3t=18,解得t=4.5,
此时,CQ=3t-10=3,BP=t=4.5,
梯形BPQC的面积为
(3+4.5)×8=30≠
×72=36.
∴不存在某一时刻t,使直线PQ能把梯形ACBO的周长和面积同时平分;
 (3)设AC中点为E,OB中点为F,连结EF,过EF中点G的直线一定能将梯形分成面积相等的两部分.
(3)设AC中点为E,OB中点为F,连结EF,过EF中点G的直线一定能将梯形分成面积相等的两部分.
∵A(0,8),C(6,8),
∴AC中点E的坐标为(3,8),
∵O(0,0),B(12,0),
∴OB中点F的坐标为(6,0),
∴EF中点G的坐标为(4.5,4).
故所求点的坐标为(4.5,4).
 解:(1)如图,作CD⊥OB于D,则四边形OACD是矩形,
解:(1)如图,作CD⊥OB于D,则四边形OACD是矩形,OD=AC=6cm,CD=AO=8cm.
在Rt△BCD中,∵∠BDC=90°,BD=OB-OD=6cm,CD=8cm,
∴BC=
| BD2+CD2 |
(2)①∵BP∥CQ,
∴当BP=CQ时,以P、B、C、Q为顶点的四边形是平行四边形.
如果0<t≤
| 10 |
| 3 |
如果
| 10 |
| 3 |
| 16 |
| 3 |
如果
| 16 |
| 3 |
综上所述,运动过程中存在t=5s或6s,以P、B、C、Q为顶点的四边形是平行四边形;
②不存在,理由如下:
∵梯形ACBO的周长和面积分别为:
周长=6+8+12+10=36(cm),面积=
| 1 |
| 2 |
若当线段PQ平分梯形ACBO的周长时,Q在AC上,则BP+BC+CQ=
| 1 |
| 2 |
即t+3t=18,解得t=4.5,
此时,CQ=3t-10=3,BP=t=4.5,
梯形BPQC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
∴不存在某一时刻t,使直线PQ能把梯形ACBO的周长和面积同时平分;
 (3)设AC中点为E,OB中点为F,连结EF,过EF中点G的直线一定能将梯形分成面积相等的两部分.
(3)设AC中点为E,OB中点为F,连结EF,过EF中点G的直线一定能将梯形分成面积相等的两部分.∵A(0,8),C(6,8),
∴AC中点E的坐标为(3,8),
∵O(0,0),B(12,0),
∴OB中点F的坐标为(6,0),
∴EF中点G的坐标为(4.5,4).
故所求点的坐标为(4.5,4).
点评:本题是四边形综合题,其中涉及到矩形的判定与性质,勾股定理,平行四边形的判定,梯形的周长与面积,中点坐标公式,综合性较强,难度适中.进行分类讨论、数形结合是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知∠1=∠2,∠3=∠4,求证:AD=BC.
如图,已知∠1=∠2,∠3=∠4,求证:AD=BC. 在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=4km,BC=2km,CD=3km,DE=3km,EF=1km,他们全部乘出租车上班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算),每辆车能容纳3人.
在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=4km,BC=2km,CD=3km,DE=3km,EF=1km,他们全部乘出租车上班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算),每辆车能容纳3人.