题目内容
18.如图,矩形ABCD中,对角线AC、BD相交于点G,E、F分别是边AD、BC的中点,AB=2,BC=4,一动点P从点B出发,沿着B-A-D-C的方向在矩形的边上运动,运动到点C停止.点M为图1中的某个定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.那么,点M的位置可能是图1中的( )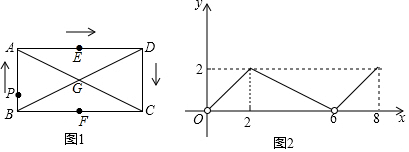
| A. | 点C | B. | 点E | C. | 点F | D. | 点G |
分析 从图2中可看出当x=6时,此时△BPM的面积为0,说明点M一定在BD上,选项中只有点G在BD上,所以点M的位置可能是图1中的点O.
解答  解:∵AB=2,BC=4,四边形ABCD是矩形,
解:∵AB=2,BC=4,四边形ABCD是矩形,
∴当x=6时,点P到达D点,此时△BPM的面积为0,说明点M一定在BD上,
∴从选项中可得只有G点符合,所以点M的位置可能是图1中的点G.
故选:D.
点评 本题主要考查了动点问题的函数图象,解题的关键是找出当x=6时,此时△BPM的面积为0,说明点M一定在BD上这一信息.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
9.如图,一个长方形是另一个长方形按顺时针方向旋转90°后形成的是( )


| A. | ①② | B. | ②④ | C. | ②③ | D. | ③④ |
6.下列运算中,正确的是( )
| A. | a6÷a2=a3 | B. | (-a)7÷(-a)3=-a4 | C. | a÷a-2=a3 | D. | ${(-5)^{-2}}=-\frac{1}{25}$ |
13.下列数学符号中,属于中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.投掷硬币m次,正面向上n次,其频率p=$\frac{n}{m}$,则下列说法正确的是( )
| A. | p一定等于$\frac{1}{2}$ | B. | p一定不等于$\frac{1}{2}$ | ||
| C. | 多投一次,p更接近$\frac{1}{2}$ | D. | 投掷次数逐步增加,p稳定在$\frac{1}{2}$附近 |
10.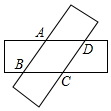 如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得点A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )
如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得点A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )
 如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得点A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )
如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得点A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )| A. | 5cm | B. | 4.8cm | C. | 4.6cm | D. | 4cm |