题目内容
13.计算:(1)$\sqrt{45}+\sqrt{18}-\sqrt{8}+\sqrt{125}$
(2)$\sqrt{24}+\sqrt{12}-(\sqrt{6}-\sqrt{27})$
(3)$\sqrt{1\frac{2}{3}}÷\sqrt{2\frac{1}{3}}×\sqrt{1\frac{2}{5}}$
(4)3$\sqrt{8}×(\sqrt{54}-5\sqrt{2}-2\sqrt{6})$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后去括号后合并即可;
(3)根据二次根式的乘除法则运算;
(4)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的乘法运算.
解答 解:(1)原式=3$\sqrt{5}$+3$\sqrt{2}$-2$\sqrt{2}$+5$\sqrt{5}$
=8$\sqrt{5}$+$\sqrt{2}$;
(2)原式=2$\sqrt{6}$+2$\sqrt{3}$-$\sqrt{6}$+3$\sqrt{3}$
=$\sqrt{6}$+5$\sqrt{3}$;
(3)原式=$\sqrt{\frac{5}{3}×\frac{3}{7}×\frac{7}{5}}$
=1;
(4)原式=6$\sqrt{2}$(3$\sqrt{6}$-5$\sqrt{2}$-2$\sqrt{6}$)
=6$\sqrt{2}$($\sqrt{6}$-5$\sqrt{2}$)
=12$\sqrt{3}$-60.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
4.-|-2|的相反数的倒数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
3.已知点A(-2,1),B(1,4),若反比例函数y=$\frac{k}{x}$与线段AB有公共点时,k的取值范围是( )
| A. | -$\frac{9}{4}$≤k<0或0<k≤4 | B. | k≤-2或k≥4 | C. | -2≤k<0或k≥4 | D. | -2≤k<0或0<k≤4 |
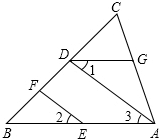 (1)如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.
(1)如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.