题目内容
5．阅读下列材料：某农民家里有一块四边形的土地要均分给两个儿子，采用的方法如下：连接AC，取AC的中点E，连接DE、BE，△AED，△ECD的等底等高，故面积也相等，同样，试△AEB、△ECB的面积也相等，把四边形ABED分给其中的一个儿子，余下的分给另一个儿子．（注：△是指三角形）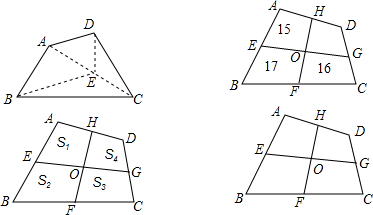
应用：在四边形ABCD中，点E，F，G，H，分别是AB，BC，CD，DE的中点．EG与FH相交于O点．
（1）若四边形AEOH、BEOF、CFOG的面积为15，17，16，则四边形DGOH的面积是14；
（2）若四边形AEOH、BEOF、CFOG、DGOH的面积分别为S1、S2、S3、S4，直接写出S1、S2、S3、S4S1+S3=S2+S4．
分析 由阅读材料可知：三角形的中线将三角形分成面积相等的两部分．条件中出现了线段的中点，问题中涉及到面积，由此联想到“三角形的中线将三角形分成面积相等的两部分”，故而连接OA、OB、OC、OD，即可得到S△AOE=S△BOE，S△BOF=S△COF，S△COG=S△DOG，S△DOH=S△AOH．
（1）由题可得S△AOE+S△AOH=15①，S△BOE+S△BOF=17②，S△COF+S△COG=16③，只需将①+③-②，就可解决问题；
（2）由题可得S△AOE+S△AOH=S1，S△BOE+S△BOF=S2，S△COF+S△COG=S3，S△DOG+S△DOH=S4，而S1+S3=S△AOE+S△AOH+S△COF+S△COG，S2+S4=S△BOE+S△BOF+S△DOG+S△DOH，即可得到S1+S3=S2+S4．
解答 解：（1）连接OA、OB、OC、OD，如图1，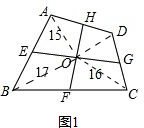
∵点E，F，G，H，分别是AB，BC，CD，DE的中点，
∴S△AOE=S△BOE，S△BOF=S△COF，S△COG=S△DOG，S△DOH=S△AOH，
∵S△AOE+S△AOH=15①，S△BOE+S△BOF=17②，S△COF+S△COG=16③，
∴由①+③-②得S△AOH+S△COG=15+16-17=14，
∴S四边形DGOH=S△DOH+S△DOG=S△AOH+S△COG=14．
故答案为14；
（2）连接OA、OB、OC、OD，如图2，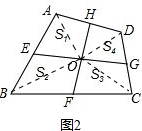
∵点E，F，G，H，分别是AB，BC，CD，DE的中点，
∴S△AOE=S△BOE，S△BOF=S△COF，S△COG=S△DOG，S△DOH=S△AOH．
∵S△AOE+S△AOH=S1，S△BOE+S△BOF=S2，S△COF+S△COG=S3，S△DOG+S△DOH=S4，
∴S1+S3=S△AOE+S△AOH+S△COF+S△COG，S2+S4=S△BOE+S△BOF+S△DOG+S△DOH，
∴S1+S3=S2+S4．
故答案为S1+S3=S2+S4．
点评 本题主要考查了“三角形的中线将三角形分成面积相等的两部分”的应用，由线段的中点联想到三角形的中线将三角形分成面积相等的两部分，是解决本题的关键．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
一个正方体的平面展开图如图所示，将它折成正方体后“建”字对面是作．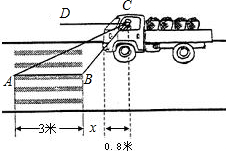
如图，一位驾驶员看到前方斑马线上有行人横穿马路，采取紧急刹车，汽车滑行12米距离后停下，
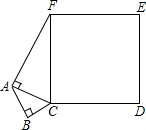如图，BC=3，AB=4，AF=12，∠FAC和∠ABC都为直角，求正方形FCDE的面积．| A． |  | B． |  | ||
| C． |  | D． |  |
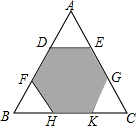如图，要把边长为12的正三角形纸板剪去三个小正三角形，得到正六边形，则剪去的小三角形这边长是多少．
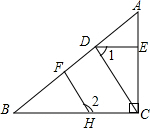如图，已知AC⊥BC，CD⊥AB，DE⊥AC，∠1+∠2=180°．求证：HF⊥AB．
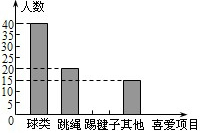某学校为了解学生大课间体育活动情况，随机抽取本校100名学生进行调查，整理收集到的数据，绘制成如图所示的统计图．若该校共有1000名学生，估计喜欢“踢毽子”的学生有250人．