题目内容
11.已知二次函数y=2x2+(2a-b)x+b.当且仅当1<x<2时,y<0.则二次函数解析式y=2x2-6x+4.分析 根据仅当1<x<2时,y<0可知:1和2是方程2x2+(2a-b)x+b=0的两个根,则图象过(1,0)和(2,0)两点,分别代入即可求出a和b的值,写出解析式.
解答 解:∵当1<x<2时,y<0,
∴二次函数图象过(1,0)和(2,0)两点,
把(1,0)和(2,0)代入y=2x2+(2a-b)x+b得:$\left\{\begin{array}{l}{2+2a-b+b=0}\\{8+2(2a-b)+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=4}\end{array}\right.$,
∴二次函数解析式为:y=2x2+(-2-4)x+4=2x2-6x+4.
点评 本题考查了二次函数的图象与一元二次方程的关系,即抛物线与x轴交点的问题;二次函数y=ax2+bx+c与x轴的交点为(x1,0)、(x2,0),则方程ax2+bx+c=0的两个根是x1和x2;反之也成立.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
6.不等式-4x<8的解集是( )
| A. | x>-2 | B. | x<2 | C. | x<-2 | D. | x>2 |
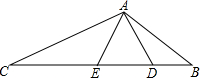 如图,已知在△ABC中,D、E在BC边上,△ADE是等边三角形,∠BAC=120°.如果BD=4,EC=9,那么△ADE的周长为18.
如图,已知在△ABC中,D、E在BC边上,△ADE是等边三角形,∠BAC=120°.如果BD=4,EC=9,那么△ADE的周长为18. 如图,已知直线y=mx+b(m≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于A(-3,-1)与B(n,6)两点,连接OA、OB.
如图,已知直线y=mx+b(m≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于A(-3,-1)与B(n,6)两点,连接OA、OB.