Question

16．已知△ABC的AB边长为4，AC边长为8，则BC边上的中线AD的长度的取值范围是2＜AD＜6．

Answer 1

分析 过点D作DE∥AB交AC于点E，根据中线的定义可得出BD=CD，根据平行线的性质即可得出DE是△ABC的中位线，由此可得出AE、DE的长度，再在△ADE中，利用三角形的三边关系即可得出AD的长度的取值范围．

解答 解：过点D作DE∥AB交AC于点E，如图所示．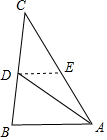
∵AD是边BC上的中线，
BD=CD，
又∵DE∥AB，
∴DE是△ABC的中位线，
∴AE=$\frac{1}{2}$AC=4，DE=$\frac{1}{2}$AB=2．
在△ADE中，由三角形的三边关系可得出：AE-DE＜AD＜AE+DE，
即2＜AD＜6．
故答案为：2＜AD＜6．

点评 本题考查了三角形的三边关系、三角形的中位线以及三角形的中线，根据三角形的三边关系找出第三边与其余两边的关系是解题的关键．